题目内容
已知函数y=Asin(ωx+φ),0<φ<π,函数图象上最高点为(2,
),在此最高点到相邻最低点间函数图象与x轴交于一点(6,0),求次函数解析式,并求函数最小值时x的值.
| 2 |
考点:正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:首先 根据函数的图象确定函数解析式中A、ω、φ的值,然后利用函数的解析式求出函数取最小值时的x的值.
解答:
解:函数y=Asin(ωx+φ),0<φ<π,函数图象上最高点为(2,
),
所以:当x=2时,函数的最大值为
,
则:A=
;
在此最高点到相邻最低点间函数图象与x轴交于一点(6,0),
所以:
=6-2,
解得:T=16,
则:ω=
=
;
当x=2时,函数达到最大值.
所以:
=
sin(
+φ)(0<φ<π),
所以:φ=
,
所求的函数解析式为:f(x)=
sin(
x+
),
当
x+
=2kπ-
(k∈Z)时,函数取最小值,
解得:x=16k-6(k∈Z).
故当x=16k-6时,函数取最小值.
| 2 |
所以:当x=2时,函数的最大值为
| 2 |
则:A=
| 2 |
在此最高点到相邻最低点间函数图象与x轴交于一点(6,0),
所以:
| T |
| 4 |
解得:T=16,
则:ω=
| 2π |
| T |
| π |
| 8 |
当x=2时,函数达到最大值.
所以:
| 2 |
| 2 |
| π |
| 4 |
所以:φ=
| π |
| 4 |
所求的函数解析式为:f(x)=
| 2 |
| π |
| 8 |
| π |
| 4 |
当
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
解得:x=16k-6(k∈Z).
故当x=16k-6时,函数取最小值.
点评:本题考查的知识要点:利用函数的图象求函数的解析式及函数性质的应用.属于基础题型.

练习册系列答案
相关题目
设方程ex=|ln(-x)|(其中e为自然对数的底数)的两个根分别为x1,x2,则( )
| A、x1x2<0 |
| B、x1x2=0 |
| C、x1x2>0 |
| D、0<x1x2<1 |
已知Ω={(x,y)||x|≤1,|y|≤1},A是由曲线y=x与y=x2围成的封闭区域,若向Ω上随机投一点p,则点p落入区域A的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC,则角A的大小为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
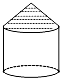 一粮仓如图所示,圆柱底面直径为12m,粮仓高4m,圆柱高与圆锥高相等,现拟建一个更大的粮仓,结构不变,现有两种方案:一是新建的仓库的底面直径比原来大2m(高不变);二是高度增加2m(底面直径不变).分别计算按这两种方案所建仓库的表面积(精确到0.01m2)
一粮仓如图所示,圆柱底面直径为12m,粮仓高4m,圆柱高与圆锥高相等,现拟建一个更大的粮仓,结构不变,现有两种方案:一是新建的仓库的底面直径比原来大2m(高不变);二是高度增加2m(底面直径不变).分别计算按这两种方案所建仓库的表面积(精确到0.01m2)