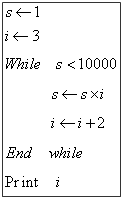题目内容
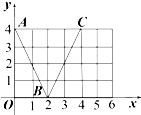如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（4，4）则| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
考点：导数的几何意义
专题：导数的概念及应用
分析：由导数的定义和几何意义可得
=f′（1）=
，计算可得．
| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
| 4-0 |
| 0-2 |
解答：
解：由导数的定义可知
=f′（1），
又f′（1）即为曲线在x=1处的切线斜率，
∴由图象可知f′（1）=
=-2，
∴
=-2；
故答案为：-2．
| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
又f′（1）即为曲线在x=1处的切线斜率，
∴由图象可知f′（1）=
| 4-0 |
| 0-2 |
∴
| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
故答案为：-2．
点评：本题考查导数的定义和几何意义，属基础题．
练习册系列答案
相关题目
y=cosx（cosx+sinx）的值域是（ ）
| A、[-2，2] | ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[-
|