题目内容
y=cosx(cosx+sinx)的值域是( )
| A、[-2,2] | ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[-
|
考点:三角函数中的恒等变换应用,三角函数的最值
专题:三角函数的图像与性质
分析:先利用二倍角公式和两角和公式对函数解析式化简,根据正弦函数的性质求得函数的最大和最小值,则函数的值域可得.
解答:
解:y=cosx(cosx+sinx)=cos2x+sinxcosx=
cos2x+
sin2x+
=
sin(2x+
)+
,
∴ymax=
,ymin=
,
∴函数的值域为:[
,
],
故选:C.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴ymax=
| ||
| 2 |
1-
| ||
| 2 |
∴函数的值域为:[
1-
| ||
| 2 |
1+
| ||
| 2 |
故选:C.
点评:本题主要考查了利用二倍角公式和两角和与差的正弦函数的公式化简求值,三角函数图象与性质.基础性较强.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
已知a,b,c为实数,下列命题正确的是( )
| A、若a>b,则ac>bc |
| B、若a>b,c>d则ac>bd |
| C、若ac2>bc2,则a>b |
| D、若a>b,c>d则a-c>b-d |
已知一个算法,其流程图如图所示,则输出的结果是( )


| A、3 | B、9 | C、27 | D、81 |
已知3,a,13成等差数列,实数c,9,27成等比数列,则a+c的值是( )
| A、11 | B、12 | C、13 | D、14 |
若0<a<
,则下列不等式中正确的是( )
| 1 |
| 2 |
A、loga(1-
| ||
B、ax≤(
| ||
| C、cos(1+α)<cos(1-α) | ||
| D、(1-a)n<an(n∈N*) |
设x∈(0,π),则函数y=sinx+
的最小值是( )
| 1 |
| sinx |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
已知cosα=
,且0<α<π,则tan(α+
)=( )
| 4 |
| 5 |
| π |
| 4 |
A、
| ||
| B、7 | ||
C、-
| ||
| D、-7 |
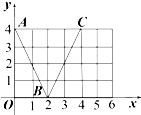 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4)则
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4)则