题目内容
若
=2012,则
+tan2α= .
| 1+tanα |
| 1-tanα |
| 1 |
| cos2α |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由条件求得tanα 的值,再利用同角三角函数的基本关系花间要求的式子为=
,计算求得结果.
| (1+tanα)2 |
| 1-tan2α |
解答:
解:∵
=2012,∴tanα=
,
∴
+tan2α=
+
=
+
=
=
=
=2012,
故答案为:2012.
| 1+tanα |
| 1-tanα |
| 2011 |
| 2013 |
∴
| 1 |
| cos2α |
| cos2α+sin2α |
| cos2α-sin2α |
| 2tanα |
| 1-tan2α |
| 1+tan2α |
| 1-tan2α |
| 2tanα |
| 1-tan2α |
| (1+tanα)2 |
| 1-tan2α |
=
(1+
| ||
1-(
|
| (2013+2011)2 |
| 20132-20112 |
故答案为:2012.
点评:本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a,b,c为实数,下列命题正确的是( )
| A、若a>b,则ac>bc |
| B、若a>b,c>d则ac>bd |
| C、若ac2>bc2,则a>b |
| D、若a>b,c>d则a-c>b-d |
设x∈(0,π),则函数y=sinx+
的最小值是( )
| 1 |
| sinx |
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
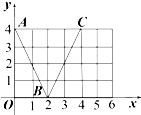 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4)则
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4)则