题目内容

已知a，b＞0，a+b=1，求8a2b+8ab2的最大值．
考点：基本不等式
专题：不等式的解法及应用
分析：根据基本不等式的性质计算即可．
解答： 解：∵a，b＞0，a+b=1，
∴8a2b+8ab2=8ab（a+b）=8ab
∵8ab≤8(
a+b
2
)2=2．当且仅当a=b=
1
2
时等号成立．
∴8a2b+8ab2的最大值为2．
点评：本题主要考查了基本不等式的应用，注意等号成立的条件．
练习册系列答案
相关题目
设数列{an}满足：a1=2，对一切正整数n，都有an+1+an=3×2n．
（1）探讨数列{an}是否为等比数列，并说明理由；
（2）设bn=
an+1
an-1
，求证：b1+b2+…+bn＜n+4．
某研究机构对高二文科学生的记忆力x和判断力y进行统计分析，得下表数据
X 6 8 10 12
Y 2 3 5 6
（1）请画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
y
=
b
x+
a
；
（3）试根据（2）求出的线性回归方程，预测记忆力为14的同学的判断力．
已知tanx=2
（1）求
sinx-cosx
sinx+cosx
的值
（2）求cos2x-sin2x的值．
已知圆C经过点M（-2，0），N（2，0），且圆心C在直线y=x上．
（Ⅰ）求圆C的方程；
（Ⅱ）若过点（2，1）的直线l1与圆C相切，求直线l1的方程；
（Ⅲ）若直线l2：y=kx+3与圆C交于A，B两点，在圆C上是否存在一点Q，使得
OQ
=
OA
+
OB
，若存在，求出此时直线l2的斜率；若不存在，说明理由．
已知集合A={x|x2+5x-6≤0}，B={x|x2+3x≥0}，求A∩B和A∪B．
已知关于x的不等式ax2+bx+1＞0的解集为（-1，
1
3
），求不等式bx2+ax＜-9的解集．
已知函数f（x）是定义在R上的奇函数，当x＞0时，f（x）=e-x（x-1），给出以下命题：
①当x＜0时，f（x）=ex（x+1）；     
②函数f（x）有五个零点；
③对?x1，x2∈R，|f（x2）-f（x1）|＜2恒成立．
④若关于x的方程f（x）=m有解，则实数m的取值范围是f（-2）≤m≤f（2）；
其中，正确命题的序号是
 
．
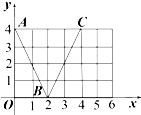如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（4，4）则
lim
△x→0
f(1+△x)-f(1)
△x
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网