题目内容
已知t>0,设函数f(x)=x3-
x2+3tx+1.
(Ⅰ)若f(x)在(0,2)上无极值,求t的值;
(Ⅱ)若存在x0∈(0,2),使得f(x0)是f(x)在[0,2]上的最大值,求t的取值范围;
(Ⅲ)若f(x)≤xex-m+2(e为自然对数的底数)对任意x∈[0,+∞)恒成立时m的最大值为1,求t的取
值范围.
| 3(t+1) |
| 2 |
(Ⅰ)若f(x)在(0,2)上无极值,求t的值;
(Ⅱ)若存在x0∈(0,2),使得f(x0)是f(x)在[0,2]上的最大值,求t的取值范围;
(Ⅲ)若f(x)≤xex-m+2(e为自然对数的底数)对任意x∈[0,+∞)恒成立时m的最大值为1,求t的取
值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值,导数在最大值、最小值问题中的应用
专题:计算题,分类讨论,导数的综合应用
分析:(Ⅰ)求出导数,令导数为0,再由f(x)在(0,2)上无极值,即可求得t;
(Ⅱ)对t讨论,分①当0<t<1时,②当t=1时,③当1<t<2时,④当t≥2时,求出单调区间,极值,进而确定最值,解不等式,即可得到t的范围;
(Ⅲ)运用参数分离,得到m≤xex-x3+
x2-3tx+1=x(ex-x2+
x-3t)+1对x≥0恒成立.
g(x)=ex-x2+
x-3t,x≥0,由于m的最大值为1.则g(x)=ex-x2+
x-3t≥0恒成立.
对g(x)二次求导,求出单调区间,求出极值和最值,判断g(x)的单调性,即可得到t的范围.
(Ⅱ)对t讨论,分①当0<t<1时,②当t=1时,③当1<t<2时,④当t≥2时,求出单调区间,极值,进而确定最值,解不等式,即可得到t的范围;
(Ⅲ)运用参数分离,得到m≤xex-x3+
| 3(t+1) |
| 2 |
| 3(t+1) |
| 2 |
g(x)=ex-x2+
| 3(t+1) |
| 2 |
| 3(t+1) |
| 2 |
对g(x)二次求导,求出单调区间,求出极值和最值,判断g(x)的单调性,即可得到t的范围.
解答:
解:(Ⅰ)f′(x)=3x2-3(t+1)x+3t=3(x-1)(x-t),
令f′(x)=0,则x=1或t,
又f(x)在(0,2)无极值,由于1∈(0,2),则t=1;
(Ⅱ)①当0<t<1时,f(x)在(0,t)单调递增,在(t,1)单调递减,在(1,2)单调递增,
∴f(t)≥f(2),由f(t)≥f(2)得:-t3+3t2≥4在0<t<1时无解.
②当t=1时,不合题意;
③当1<t<2时,f(x)在(0,1)单调递增,在(1,t)单调递减,在(t,2)单调递增,
∴
即
∴
≤t<2;
④当t≥2时,f(x)在(0,1)单调递增,在(1,2)单调递减,满足条件.
综上所述:t∈[
,+∞)时,存在x0∈(0,2),使得f(x0)是f(x)在[0,2]上的最大值.
(Ⅲ)若f(x)≤xex-m+2(e为自然对数的底数)对任意x∈[0,+∞)恒成立,
即m≤xex-x3+
x2-3tx+1=x(ex-x2+
x-3t)+1对x≥0恒成立.
令g(x)=ex-x2+
x-3t,x≥0,由于m的最大值为1.
则g(x)=ex-x2+
x-3t≥0恒成立,否则?x0>0,g(x0)<0,
则当x=x0,m=1时,f(x)≤xex-m+2不恒成立,
由于g(0)=1-3t≥0,则0<t≤
,
当0<t≤
时,g′(x)=ex-2x+
,则g′′(x)=ex-2;
若g′′(x)=0,则x=ln2,则g′(x)在(0,ln2)上递减,
在(ln2,+∞)上递增,则g′(x)min=g′(ln2)=2+
-ln2>0,
则g(x)在x≥0上递增,则g(x)≥g(0)=1-3t≥0,满足条件,
故t的取值范围是(0,
].
令f′(x)=0,则x=1或t,
又f(x)在(0,2)无极值,由于1∈(0,2),则t=1;
(Ⅱ)①当0<t<1时,f(x)在(0,t)单调递增,在(t,1)单调递减,在(1,2)单调递增,
∴f(t)≥f(2),由f(t)≥f(2)得:-t3+3t2≥4在0<t<1时无解.
②当t=1时,不合题意;
③当1<t<2时,f(x)在(0,1)单调递增,在(1,t)单调递减,在(t,2)单调递增,
∴
|
|
| 5 |
| 3 |
④当t≥2时,f(x)在(0,1)单调递增,在(1,2)单调递减,满足条件.
综上所述:t∈[
| 5 |
| 3 |
(Ⅲ)若f(x)≤xex-m+2(e为自然对数的底数)对任意x∈[0,+∞)恒成立,
即m≤xex-x3+
| 3(t+1) |
| 2 |
| 3(t+1) |
| 2 |
令g(x)=ex-x2+
| 3(t+1) |
| 2 |
则g(x)=ex-x2+
| 3(t+1) |
| 2 |
则当x=x0,m=1时,f(x)≤xex-m+2不恒成立,
由于g(0)=1-3t≥0,则0<t≤
| 1 |
| 3 |
当0<t≤
| 1 |
| 3 |
| 3(t+1) |
| 2 |
若g′′(x)=0,则x=ln2,则g′(x)在(0,ln2)上递减,
在(ln2,+∞)上递增,则g′(x)min=g′(ln2)=2+
| 3(t+1) |
| 2 |
则g(x)在x≥0上递增,则g(x)≥g(0)=1-3t≥0,满足条件,
故t的取值范围是(0,
| 1 |
| 3 |
点评:本题考查导数的运用:求单调区间和求极值、最值,考查分类讨论的思想方法,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
已知a=log23,b=log
5,c=(
)0.3则( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、a<c<b |
| C、b<c<a |
| D、b<a<c |
若点N在直线1上,直线l又在平面α内,则点N,直线l与平面α之间的关系可记作( )
| A、N∈l∈α |
| B、N∈l?α |
| C、N?l?α |
| D、N?l∈α |
数列{an}的通项公式an=
(n∈N*),若前n项和为Sn,则Sn为( )
| 1 | ||||
|
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
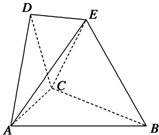 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上. 如图,△ABC为正三角形,EC⊥平面ABC,BD⊥平面ABC,CE=CA=2BD,M是EA的中点,N是EC的中点,求证:平面DMN∥平面ABC.
如图,△ABC为正三角形,EC⊥平面ABC,BD⊥平面ABC,CE=CA=2BD,M是EA的中点,N是EC的中点,求证:平面DMN∥平面ABC.