题目内容
11.三棱锥D-ABC的三个侧面分别与底面全等,且AB=AC=$\sqrt{3}$,BC=2,则二面角A-BC-D的大小为90°.分析 取BC的中点E,连接AE、DE,则∠AED为二面角A-BC-D的平面角,由此能求出二面角A-BC-D的大小.
解答 解:如图,三棱锥D-ABC的三个侧面分别与底面全等,且AB=AC=$\sqrt{3}$,BC=2,
∴DB=DC=$\sqrt{3}$,AD=2,取BC的中点E,连接AE、DE,
则DE⊥BC,AE⊥BC,
∴∠AED为二面角A-BC-D的平面角.
∵AE=DE=$\sqrt{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{2}$,
∴AE2+DE2=AD2.
∴∠AED=90°.
∴二面角A-BC-D的大小为90°.
故答案为:90°.
点评 本题考查二面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
6.设a=log32,b=2-1,c=log56,则( )
| A. | a<c<b | B. | b<c<a | C. | b<a<c | D. | a<b<c |
16.三棱柱各面所在平面将空间分成( )部分.
| A. | 18 | B. | 21 | C. | 24 | D. | 27 |
20.过点A(2,b)和点B(3,-2)的直线的斜率为-1,则b的值是( )
| A. | 5 | B. | 1 | C. | -5 | D. | -1 |
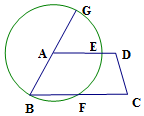 在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.
在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.