题目内容
13.已知函数f(x)满足$2f({\frac{x-1}{x}})+f({\frac{x+1}{x}})=1+x$,其中x∈R且x≠0,则函数f(x)的解析式为f(x)=$\frac{1}{3}$-$\frac{1}{x-1}$(x≠1).分析 以-x代入可得2f($\frac{x+1}{x}$)+f($\frac{x-1}{x}$)=1-x,与已知方程联立可得f($\frac{x+1}{x}$)=$\frac{1}{3}$-x,再利用换元法,即可得出结论.
解答 解:以-x代入可得2f($\frac{x+1}{x}$)+f($\frac{x-1}{x}$)=1-x,
与已知方程联立可得f($\frac{x+1}{x}$)=$\frac{1}{3}$-x,
令t=$\frac{x+1}{x}$,t≠1,x=$\frac{1}{t-1}$,∴f(t)=$\frac{1}{3}$-$\frac{1}{t-1}$,
∴f(x)=$\frac{1}{3}$-$\frac{1}{x-1}$(x≠1).
故答案为f(x)=$\frac{1}{3}$-$\frac{1}{x-1}$(x≠1).
点评 本题考查函数解析式的求解,考查方程组思想,考查换元法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.函数y=ax-1(a>0且a≠1)恒过定点( )
| A. | (0,1) | B. | (1,1) | C. | (1,0) | D. | (2,1) |
8.设命题p:?x∈R,x2<2015,则¬p为( )
| A. | ?x∈R,x2≥2015 | B. | ?x∈R,x2<2015 | C. | ?x∈R,x2≥2015 | D. | ?x∈R,x2>2015 |
5.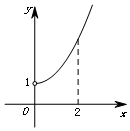 已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )
 已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )| A. | y=x2+1 | B. | y=log2|x| | ||
| C. | y=$\left\{\begin{array}{l}{{e}^{x}(x≥0)}\\{{e}^{-x}(x<0)}\end{array}\right.$ | D. | y=|x+2| |
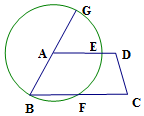 在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.
在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.