题目内容
15.数列{an}中,a1=3,an+1=2an+2(n∈N*).(1)求a2,a3的值;
(2)求证:{an+2}是等比数列,并求数列{an}的通项公式;
(3)设bn=$\frac{n}{{a}_{n}+2}$,Sn=b1+b2+…+bn,证明:对?n∈N*,都有$\frac{1}{5}$≤Sn<$\frac{4}{5}$.
分析 (1)a1=3,an+1=2an+2(n∈N*).取n=1,2即可得出.
(2)由an+1=2an+2(n∈N*).得an+1+2=2(an+2)利用等比数列的定义及其通项公式即可得出.
(3)由(1)可得:bn=$\frac{n}{5×{2}^{n-1}}$,利用“错位相减法”与等比数列的求和公式、数列的单调性即可得出.
解答 解:(1)a1=3,an+1=2an+2(n∈N*).
则a2=2×3+2=8,a3=2×8+2=18.
(2)证明:由an+1=2an+2(n∈N*).得an+1+2=2(an+2),∵a1=3,a1+2=5,
∴{an+2}是首项为5,公比为2的等比数列,
an+2=5×2n-1,∴an=5×2n-1-2.
(3)证明:由(1)可得:bn=$\frac{n}{5×{2}^{n-1}}$,
Sn=$\frac{1}{5}$$(1+\frac{2}{2}+\frac{3}{{2}^{2}}+…+\frac{n}{{2}^{n-1}})$①
$\frac{1}{2}{S}_{n}$=$\frac{1}{5}$$(\frac{1}{2}+\frac{2}{{2}^{2}}+\frac{3}{{2}^{3}}+…+\frac{n}{{2}^{n}})$②
①-②可得:Sn=$\frac{2}{5}$$(1+\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}}-\frac{n}{{2}^{n}})$=$\frac{2}{5}(\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}-\frac{n}{{2}^{n}})$=$\frac{2}{5}$$(2-\frac{2+n}{{2}^{n}})$.
∴Sn$<\frac{4}{5}$.
又∵Sn+1-Sn=$\frac{2}{5}×\frac{n+1}{{2}^{n+1}}$>0,
∴数列{Sn}单调递增,Sn≥S1=$\frac{1}{5}$,
∴对?n∈N*,都有$\frac{1}{5}$≤Sn<$\frac{4}{5}$.
点评 本题考查了“错位相减法”、等比数列的通项公式与求和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案| A. | a<c<b | B. | b<c<a | C. | b<a<c | D. | a<b<c |
| A. | 5 | B. | 1 | C. | -5 | D. | -1 |
| A. | (0,1) | B. | (1,1) | C. | (1,0) | D. | (2,1) |
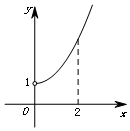 已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )| A. | y=x2+1 | B. | y=log2|x| | ||
| C. | y=$\left\{\begin{array}{l}{{e}^{x}(x≥0)}\\{{e}^{-x}(x<0)}\end{array}\right.$ | D. | y=|x+2| |
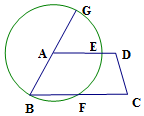 在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.
在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.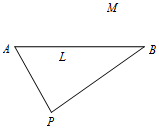 我边防局接到情报,在海礁AB所在直线l的一侧点M处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕.如图,已知快艇出发位置在l的另一侧码头P处,PA=8公里,PB=10公里,∠APB=60°.
我边防局接到情报,在海礁AB所在直线l的一侧点M处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕.如图,已知快艇出发位置在l的另一侧码头P处,PA=8公里,PB=10公里,∠APB=60°.