sin63°cos18°+cos63°cos108°=$\frac{{\sqrt{2}}}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

14．sin63°cos18°+cos63°cos108°=$\frac{{\sqrt{2}}}{2}$．

分析利用诱导公式，两角差的正弦函数公式，特殊角的三角函数值即可化简求值得解．

解答解：sin63°cos18°+cos63°cos108°
=sin63°cos18°+cos63°cos（90°+18°）
=sin63°cos18°-cos63°sin18°
=sin（63°-18°）
=sin45°
=$\frac{{\sqrt{2}}}{2}$．
故答案为：$\frac{{\sqrt{2}}}{2}$．

点评本题主要考查了诱导公式，两角差的正弦函数公式，特殊角的三角函数值在解三角形中的应用，考查了转化思想，属于基础题．

练习册系列答案

12．（1）已知函数f（x）=x³-mx²-nx的图象与x轴相切，切点为（1，0），且g（x）=f（x）+1，求g（x）的极值．
（2）已知f（x）=ax²+bx+c（a≠0），且f（-1）=2，f'（0）=0，$\int_{\;-1}^{\;0}{f（x）dx=-4}$，求a、b、c的值．

2．已知F₁，F₂为椭圆$\frac{{x}^{2}}{4}$+y²=1的左右焦点，弦AB过F₁，则△F₂AB的周长为（　　）

9．在平面直角坐标系中，点P为曲线C上任意一点，且P到定点F（1，0）的距离比到y轴的距离多1．
（1）求曲线C的方程；
（2）点M为曲线C上一点，过点M分别作倾斜角互补的直线MA，MB与曲线C分别交于A，B两点，过点F且与AB垂直的直线l与曲线C交于D，E两点，若|DE|=8，求点M的坐标．

19．过抛物线y²=4x焦点的直线l交抛物线于P（x₁，x₂），Q（x₂，y₂）两点，若x₁+x₂=6，则|PQ|=（　　）

6．设a=log₃2，b=2^-1，c=log₅6，则（　　）

3．

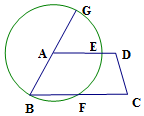在梯形ABCD中，AD∥BC∠BAD=135°，以A为圆心，AB为半径，作⊙A交AD、BC于E、F两点，并交BA延长线于G点，则$\widehat{BF}$的度数是90°．

4．函数y=a^x-1（a＞0且a≠1）恒过定点（　　）

试题分类