题目内容
8.直线l的斜率k为$-\frac{3}{4}$,则直线l的倾斜角为π-arctan$\frac{3}{4}$.分析 设直线l的倾斜角为θ,θ∈[0,π).由k=tanθ=-$\frac{3}{4}$,即可得出.
解答 解:设直线l的倾斜角为θ,θ∈[0,π).
∵k=tanθ=-$\frac{3}{4}$,
∴θ=π-arctan$\frac{3}{4}$.
故答案为:π-arctan$\frac{3}{4}$.
点评 本题考查了直线的倾斜角与斜率的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
5.已知z=(m+3)+(m-1)i在复平面内对应的点在第三象限,则实数m的取值范围是( )
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
16.三棱柱各面所在平面将空间分成( )部分.
| A. | 18 | B. | 21 | C. | 24 | D. | 27 |
20.过点A(2,b)和点B(3,-2)的直线的斜率为-1,则b的值是( )
| A. | 5 | B. | 1 | C. | -5 | D. | -1 |
17.函数$y=\sqrt{2sin(π-2x)-1}$的定义域为( )
| A. | $\{x|2kπ+\frac{π}{6}≤x≤2kπ+\frac{5π}{6},k∈Z\}$ | B. | $\{x|kπ+\frac{π}{6}≤x≤kπ+\frac{5π}{6},k∈Z\}$ | ||
| C. | $\{x|2kπ+\frac{π}{3}≤x≤2kπ+\frac{2π}{3},k∈Z\}$ | D. | $\{x|kπ+\frac{π}{12}≤x≤kπ+\frac{5π}{12},k∈Z\}$ |
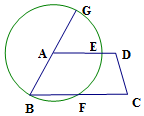 在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.
在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.