题目内容

16．设Sn是等差数列{an}的前n项和，若a3+a5+a7=27，则S9=（　　）
A．81B．79C．77D．75

分析 利用等差数列的性质求和公式即可得出．

解答 解：∵数列{an}是等差数列，a3+a5+a7=27，∴3a5=27，解得a5=9．
则S9=$\frac{9（{a}_{1}+{a}_{9}）}{2}$=9a5=81．
故选：A．

点评 本题考查了等差数列的性质求和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
6．已知直线2x-$\sqrt{3}$y=0为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的一条渐近线，则该双曲线的离心率为$\frac{\sqrt{21}}{3}$．
7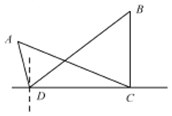．如图所示，为了测量A，B处岛屿的距离，小明在D处观测，A，B分别在D处的北偏西15°、北偏东45°方向，再往正东方向行驶40海里至C处，观测B在C处的正北方向，A在C处的北偏西60°方向，则A，B两处岛屿间的距离为（　　）
A．$20\sqrt{6}$海里B．$40\sqrt{6}$海里C．$20（1+\sqrt{3}）$海里D．40海里
4．在平面直角坐标系中，角α的顶点与原点O重合，始边与x轴的非负半轴重合，点P（-2t，t）（t≠0）是角α终边上的一点，则$tan（α+\frac{π}{4}）$的值为（　　）
A．$3-2\sqrt{2}$B．3C．$-\frac{1}{3}$D．$\frac{1}{3}$
11．从集合{2，3，4，5}中随机抽取一个数a，从集合{4，6，8}中随机抽取一个数b，则向量$\overrightarrow{m}$=（a，b）与向量$\overrightarrow{n}$=（-2，1）垂直的概率为$\frac{1}{4}$．
1．若函数f（x）=1nx-$\frac{1}{e^2}$x+a有零点，则实数a的取值范围是（　　）
A．（-∞，-1]B．（-∞，1]C．[-1，+∞）D．[1，+∞）
8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率为$\frac{\sqrt{2}}{2}$，右焦点为F，上顶点为A，且△AOF的面积为$\frac{1}{2}$（O为坐标原点）．
（1）求椭圆C的方程；
（2）若点M在以椭圆C的短轴为直径的圆上，且M在第一象限，过M作此圆的切线交椭圆于P，Q两点．试问△PFQ的周长是否为定值？若是，求此定值；若不是，说明理由．
5．圆x2+y2-2y=0与曲线y=|x|-1的公共点个数为（　　）
A．4B．3C．2D．0
6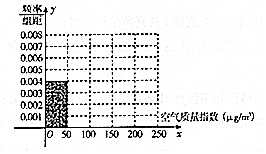．全世界人们越来越关注环境保护问题，某监测站点于2016年8月某日起连续n天监测空气质量指数（AQI），数据统计如下：
空气质量指数（μg/m3）区间[0，50）[50，100）[100，150）[150，200）[200，250）
空间质量等级空气优空气良轻度污染中度污染重度污染
天数2040m105
（1）根据所给统计表和频率分布直方图中的信息求出n，m的值，并完成频率分布直方图；
（2）由频率分布直方图求该组数据的平均数与中位数；
（3）在空气质量指数分别属于[50，100）和[150，200）的监测数据中，用分层抽样的方法抽取5天，再从中任意选取2天，求事件A”两天空气都为良“发生的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网