题目内容
1.若函数f(x)=1nx-$\frac{1}{e^2}$x+a有零点,则实数a的取值范围是( )| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
分析 判断f(x)的单调性,求出f(x)的极值,比较极值与0的关系得出a的范围.
解答 解:f′(x)=$\frac{1}{x}-\frac{1}{{e}^{2}}$,
∴当0<x<e2时,f′(x)>0,当x>e2时,f′(x)<0,
∴f(x)在(0,e2)上单调递增,在(e2,+∞)上单调递减,
∴当x=e2时,f(x)取得最大值f(e2)=1+a,
∵f(x)有零点,且x→0时,f(x)→-∞,
∴1+a≥0,解得a≥-1.
故选C.
点评 本题考查了函数零点与函数单调性、极值的关系,属于中档题.

练习册系列答案
相关题目
16.设Sn是等差数列{an}的前n项和,若a3+a5+a7=27,则S9=( )
| A. | 81 | B. | 79 | C. | 77 | D. | 75 |
13.若复数z-i=1+i,则|z|=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 5 |



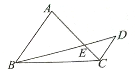 如图所示,AC与BD交于点E,AB∥CD,AC=3$\sqrt{5}$,AB=2CD=6,当tanA=2时,$\overrightarrow{BE}•\overrightarrow{DC}$=-12.
如图所示,AC与BD交于点E,AB∥CD,AC=3$\sqrt{5}$,AB=2CD=6,当tanA=2时,$\overrightarrow{BE}•\overrightarrow{DC}$=-12.