题目内容
已知f(x)=3sinx-πx,命题p:?x∈(0,
),f(x)<0,则( )
| π |
| 2 |
A、p是假命题,?p:?x∈(0,
| ||
B、p是假命题,?p:?x0∈(0,
| ||
C、p是真命题,?p:?x0∈(0,
| ||
D、p是真命题,?p:?x∈(0,
|
考点:命题的真假判断与应用,命题的否定
专题:简易逻辑
分析:通过函数的导数判断函数的单调性,判断全称命题的真假,然后写出命题的否定命题,判断真假即可得到选项.
解答:
解:因为f'(x)=3cosx-π,所以当x∈(0,
)时,f'(x)<0,函数f(x)单调递减,即对?x∈(0,
),f(x)<f(0)=0恒成立,所以p是真命题.又全称命题的否定是特称命题,所以?p是?x0∈(0,
),f(x0)≥0.
故选:C.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故选:C.
点评:本题考查函数的单调性与全称命题的否定.解题首先判断命题p的真假,然后再将命题p写成?p的形式,注意特称命题与全称命题否定形式的基本格式.

练习册系列答案
相关题目
已知命题p:?x∈R,x2+2ax+2-a=0为真命题,则实数a的取值范围是( )
| A、a≥1或a≤-2 |
| B、a≤-2或1≤a≤2 |
| C、a≥1 |
| D、-2≤a≤1 |
已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+2-x,则f(2)+g(2)=( )
| A、4 | B、-4 | C、2 | D、-2 |
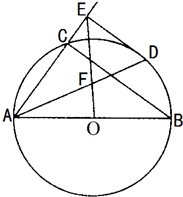 如图所示,⊙O的直径为AB,AD平分∠BAC,AD交⊙O于点D,BC∥DE,且DE交AC的延长线于点E,OE交AD于点F.
如图所示,⊙O的直径为AB,AD平分∠BAC,AD交⊙O于点D,BC∥DE,且DE交AC的延长线于点E,OE交AD于点F.