题目内容
 某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为1,顶角为2α的等腰三角形.
某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为1,顶角为2α的等腰三角形.(Ⅰ)若角2α=
| 2π |
| 3 |
(Ⅱ)写出α的取值范围,当α取何值时该八边形的面积最大,并求出最大面积.
考点:函数解析式的求解及常用方法,函数的最值及其几何意义
专题:计算题,解题方法
分析:(1)根据正弦定理可先求出4个三角形的面积,再由余弦定理可求出正方形的边长进而得到面积,最后得到答案.
(2)利用三角函数把2sin2α-2cos2α=
(
sin2α-
cos2α)=
(cos
sin2α-sin
cos2α)=
sin(2α-
),在利用2α的范围求出(2α-
)的范围,问题得以解决.
(2)利用三角函数把2sin2α-2cos2α=
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:
解:(Ⅰ)由正弦定理可得4个等腰三角形的面积和为:4×
×1×1×sinα=2sin2α,
由余弦定理可得正方形边长为:
=
,
故正方形面积为:2-2cos2α,
所以所求八边形的面积为:2sin2α-2cos2α+2,
当2α=
时,
所以所求八边形的面积为:2sin
π-2cos
π+2=3+
.
(Ⅱ)设八边形的面积为S,由(Ⅰ)所求八边形的面积为:S=2sin2α-2cos2α+2=2+2
sin(2α-
),
显然0<2α<π,所以0<α<
, ∴-
<2α-
<
π,
故-
<sin(2α-
)≤1
∴Smax=2+2
,
此时α=
π.
| 1 |
| 2 |
由余弦定理可得正方形边长为:
| 12+12-2×1×1×cos2α |
| 2-co2α |
故正方形面积为:2-2cos2α,
所以所求八边形的面积为:2sin2α-2cos2α+2,
当2α=
| 2π |
| 3 |
所以所求八边形的面积为:2sin
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
(Ⅱ)设八边形的面积为S,由(Ⅰ)所求八边形的面积为:S=2sin2α-2cos2α+2=2+2
| 2 |
| π |
| 4 |
显然0<2α<π,所以0<α<
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 4 |
故-
| ||
| 2 |
| π |
| 4 |
∴Smax=2+2
| 2 |
此时α=
| 3 |
| 8 |
点评:本题考查了三角面积公式的应用和余弦定理的应用,正、余弦定理是考查解三角形的重点,是必考内容.

练习册系列答案
相关题目
 定义一种运算符号“?”,两个实数a,b的“a?b”运算原理如图所示,若输人a=2cos
定义一种运算符号“?”,两个实数a,b的“a?b”运算原理如图所示,若输人a=2cos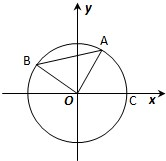 如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围.
如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围.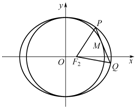 已知椭圆
已知椭圆