题目内容
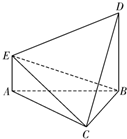 如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.
如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.(Ⅰ)在线段DC上存在一点F,使得EF丄面DBC,试确定F的位置,并证明你的结论;
(Ⅱ)求二面角D-EC-B的平面角的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)首先确定点的存在的位置,进一步说明理由,采用线面垂直的性质和相关的判定,及相关的运算知识.
(Ⅱ) 首先建立空间直角坐标系,进一步求出平面的法向量,利用向量的数量积知识,求出二面角的平面角.
(Ⅱ) 首先建立空间直角坐标系,进一步求出平面的法向量,利用向量的数量积知识,求出二面角的平面角.
解答:
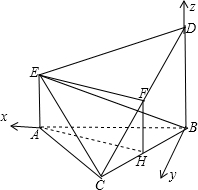 解:(Ⅰ)F在CD的中点位置.
解:(Ⅰ)F在CD的中点位置.
证明:取CD的中点F,BC的中点H,由于F、H点分别是CD和BC的中点,
所以:FH∥BD且 FH=
BD,
AE=FH,AE∥FH,
所以:四边形AHFE为平行四边形.
由DB丄平面ABC,
所以:BD⊥AH,AH⊥BC,
所以:AH⊥平面BCD,
由于EF∥AH,
所以:EF⊥平面BCD.
(Ⅱ)如图建立空间直角坐标系,则:C(1,
,0),B(0,0,0),E(2,0,1),D(0,0,2),
所以:
=(2,0,1),
=(-1,
,-1),
=(2,0,-1),
设平面BCE的法向量为:
=(x1,y1,z1),
则:
解得:
=(1,-
,-2)
同理设平面CDE的法向量为:
=(x2,y2,z2)
则:
解得:
=(1,
,2)
则:利用cos<
,
>=
=-
所以:二面角D-EC-B的平面角的余弦值为
.
 解:(Ⅰ)F在CD的中点位置.
解:(Ⅰ)F在CD的中点位置.证明:取CD的中点F,BC的中点H,由于F、H点分别是CD和BC的中点,
所以:FH∥BD且 FH=
| 1 |
| 2 |
AE=FH,AE∥FH,
所以:四边形AHFE为平行四边形.
由DB丄平面ABC,
所以:BD⊥AH,AH⊥BC,
所以:AH⊥平面BCD,
由于EF∥AH,
所以:EF⊥平面BCD.
(Ⅱ)如图建立空间直角坐标系,则:C(1,
| 3 |
所以:
| BE |
| EC |
| 3 |
| DE |
设平面BCE的法向量为:
| n1 |
则:
|
解得:
| n1 |
| ||
| 3 |
同理设平面CDE的法向量为:
| n2 |
则:
|
解得:
| n2 |
| 3 |
则:利用cos<
| n1 |
| n2 |
| ||||
|
|
| ||
| 4 |
所以:二面角D-EC-B的平面角的余弦值为
| ||
| 4 |
点评:本题考查的知识要点:线面垂直的判定和性质定理,空间直角坐标系,法向量的应用,向量的数量积,二面角的应用,属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知p:方程
+
=1所表示的曲线为焦点在x轴上的椭圆,q:|t-a|<2(a∈N),若p是q的充分不必要条件,则a取值范围为( )
| x2 |
| 3-t |
| y2 |
| t+1 |
| A、(-∞,1] |
| B、[-1,1] |
| C、[0,+∞) |
| D、(0,1) |
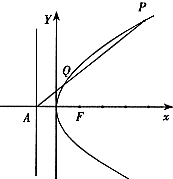 抛物线的顶点在原点,焦点在x轴上,准线l与x轴相交于点A(-1,0),过点A的直线与抛物线相交于P、Q两点.
抛物线的顶点在原点,焦点在x轴上,准线l与x轴相交于点A(-1,0),过点A的直线与抛物线相交于P、Q两点.  某海岛上有一座海拔1千米的山,山顶上有一观察站P(P在海平面上的射影点为A),测得一游艇在海岛南偏西30°,俯角为45°的B处,该游艇准备前往海岛正东方向,俯角为45°的旅游景点C处,如图所示.
某海岛上有一座海拔1千米的山,山顶上有一观察站P(P在海平面上的射影点为A),测得一游艇在海岛南偏西30°,俯角为45°的B处,该游艇准备前往海岛正东方向,俯角为45°的旅游景点C处,如图所示.