题目内容
已知函数f(x)=
(1)求
f(x);
(2若
f(x)存在,求a,b的值;
(3)若函数f(x)在x=1处连续,求a,b所满足的条件.
|
(1)求
| lim | ||
| x |
(2若
| lim | ||
| x |
(3)若函数f(x)在x=1处连续,求a,b所满足的条件.
考点:极限及其运算,分段函数的应用
专题:计算题,导数的概念及应用
分析:(1)利用极限运算得
f(x)=
=1;
(2)求左极限
f(x)=
=
=
;故从而右极限a+2=
;从而解a=-
,b任意;
(3)若函数f(x)在x=1处连续,则左右极限相等且等于在x=1的函数值,从而解得a=-
,b=
.
| lim | ||
| x |
| lim | ||
| x |
| |||
|
(2)求左极限
| lim |
| x→1- |
| lim |
| x→1- |
| |||
|
| lim |
| x→1- |
| |||||||
|
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
(3)若函数f(x)在x=1处连续,则左右极限相等且等于在x=1的函数值,从而解得a=-
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)
f(x)=
=1;
(2)
f(x)=
=
=
;
故a+2=
;
解得,a=-
,b任意;
(3)若函数f(x)在x=1处连续,
则a=-
,b=
.
| lim | ||
| x |
| lim | ||
| x |
| |||
|
(2)
| lim |
| x→1- |
| lim |
| x→1- |
| |||
|
| lim |
| x→1- |
| |||||||
|
| 3 |
| 2 |
故a+2=
| 3 |
| 2 |
解得,a=-
| 1 |
| 2 |
(3)若函数f(x)在x=1处连续,
则a=-
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了极限的运算,属于中档题.

练习册系列答案
相关题目
已知复数z1=1-i,z2=i,则z=z1•z2在复平面内对应点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知全集U={0,1,2,3,4,5,6},集合A={2,4,5},B={1,3,4,6},则(∁uA)∩B为( )
| A、{0,1,3,6} |
| B、{0,2,4,6} |
| C、{0,1,6} |
| D、{1,3,6} |
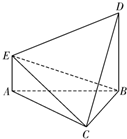 如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.
如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.