题目内容
已知sin
+2cos
=0.
(1)求tanx的值;
(2)求
的值.
| x |
| 2 |
| x |
| 2 |
(1)求tanx的值;
(2)求
| cosx+sinx |
| sinx-cosx |
考点:三角函数的化简求值
专题:计算题,三角函数的求值
分析:(1)原式移项后相除可得tan
=-2,从而可求tanx的值;
(2)根据同角三角函数关系式化简后代入求值即可.
| x |
| 2 |
(2)根据同角三角函数关系式化简后代入求值即可.
解答:
解:(1)由sin
+2cos
=0,可得 tan
=-2(2分)
所以tanx=
=
(4分)
(2)
=
(7分)
=7(8分)
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
所以tanx=
| 2×(-2) |
| 1-22 |
| 4 |
| 3 |
(2)
| cosx+sinx |
| sinx-cosx |
| 1+tanx |
| tanx-1 |
=7(8分)
点评:本题主要考察了同角三角函数关系式的应用,三角函数的化简求值,属于基本的考查.

练习册系列答案
相关题目
如果集合A={x|x≤5},a=3,那么( )
| A、{a}?A | B、a∉A |
| C、{a}∈A | D、a⊆A |
已知复数z1=1-i,z2=i,则z=z1•z2在复平面内对应点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设集合M={m∈Z|-2<m<3},N={n∈N|-1≤n≤2},则M∩N=( )
| A、{0,1} |
| B、{-1,0,1} |
| C、{0,1,2} |
| D、{-1,0,1,2} |
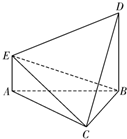 如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.
如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.