��Ŀ����
3������{an}��ʾ��n����ʱij��ϸ����������ϸ�������������µ�n�����������rn=0.6��rn=$\frac{{{a_{n+1}}-{a_n}}}{a_n}$��n��N*����������ϸ����ʵ������������ʱ������������rn�ᷢ���仯����ͼ������ϸ���������ʵ������״̬��ϸ������Q��ʱ��ı仯���ɣ���ô��������ϸ����ʵ����������������rn�Ĺ���������ȷ���ǣ�������
| A�� | 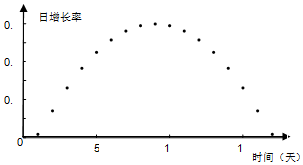 | |
| B�� | 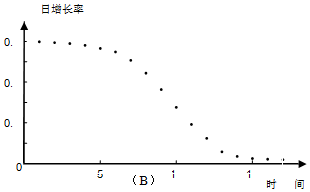 | |
| C�� | 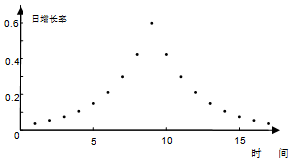 | |
| D�� | 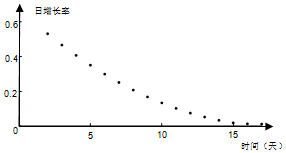 |
���� ��ͼ���֪����һ�쵽�����죬ʵ���������������غϣ�r1=r2=r6=0.6Ϊ��ֵ����ʵ������ڵ�10����������ǽ��͵ģ����ҽ��͵��ٶ��DZ�С�ģ����ɵó����ۣ�
��� �⣺��ͼ���֪����һ�쵽�����죬ʵ���������������غϣ�
r1=r2=r6=0.6Ϊ��ֵ����ʵ������ڵ�10����������ǽ��͵ģ����ҽ��͵��ٶ��DZ�С�ģ�
��ѡB��
���� ���⿼��ɢ��ͼ���������ν�ϵ���ѧ˼�룬�Ƚϻ�����

��ϰ��ϵ�д�
�����Ŀ
3����֪����y=loga��x-3��-1��a��0��a��1��ͼ�������P����ֱ��mx-ny-1=0��m��0��n��0������Pʱ����$\frac{1}{m}$+$\frac{1}{n}$����СֵΪ��������
| A�� | 4 | B�� | 2$\sqrt{2}$ | C�� | 9 | D�� | 18 |
11��һ����������100�����壬������Ϊ0��1��2��3������99�������˳��ƽ���ֳ�10��С�飬�������Ϊ1��2��3����10������ϵͳ����������ȡһ������Ϊ10������������1�������ȡ�ĺ���Ϊm=6�����ڵ�7���г�ȡ�ĺ����ǣ�������
| A�� | 66 | B�� | 76 | C�� | 63 | D�� | 73 |
18����$cos��=\frac{1}{2}$���ǡ�$��=\frac{��}{3}$���ģ�������
| A�� | ��Ҫ���� | B�� | ��ֲ���Ҫ���� | ||
| C�� | ��Ҫ��������� | D�� | �����Ҳ����Ҫ���� |
12��˫����$\frac{x^2}{16}-\frac{y^2}{8}=1$��ʵ�᳤�ǣ�������
| A�� | 2 | B�� | $4\sqrt{2}$ | C�� | $2\sqrt{2}$ | D�� | 8 |
13����������������������ij�����̳�ͨ���Դ���ǰ��20��ĵ��飬�õ������վ�������Q����20���еĵ�x�죨x��N+���IJ������������
��1�����ݱ������ݣ���Ϻ���ͼ������ʣ������к���ģ����ѡȡһ����ǡ���ĺ���ģ������Q��x�ı仯��ϵ��ֻ��˵�����ɣ�����֤����
��Q=ax+b����Q=-x2+ax+b����Q=ax+b����Q=b+logax��
��2����ϱ��е����ݣ�������ѡ��ĺ���ģ�ͣ�����ú����Ľ���ʽ����ȷ���վ���������ߵ��ǵڼ��죻�����������ֵ��
| ����x���죩 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| �վ�������Q����Ԫ�� | 154 | 180 | 198 | 208 | 210 | 204 | 190 |
��Q=ax+b����Q=-x2+ax+b����Q=ax+b����Q=b+logax��
��2����ϱ��е����ݣ�������ѡ��ĺ���ģ�ͣ�����ú����Ľ���ʽ����ȷ���վ���������ߵ��ǵڼ��죻�����������ֵ��