题目内容
12．双曲线$\frac{x^2}{16}-\frac{y^2}{8}=1$的实轴长是（ ）| A． | 2 | B． | $4\sqrt{2}$ | C． | $2\sqrt{2}$ | D． | 8 |
分析 双曲线方程$\frac{x^2}{16}-\frac{y^2}{8}=1$中，由a2=16，能求出双曲线的实轴长．
解答 解：双曲线方程$\frac{x^2}{16}-\frac{y^2}{8}=1$中，
∵a2=16，
∴双曲线的实轴长2a=2×4=8．
故选D．
点评 本题考查双曲线的实轴长的求法，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．将号码分别为1、2、…、6的六个小球放入一个袋中，这些小球仅号码不同，其余完全相同．甲从袋中摸出一个球，号码为a，放回后，乙从此袋再摸出一个球，其号码为b，则使不等式a-2b+2＞0成立的事件发生的概率等于（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
20．已知α∈（0，π），$cosα=-\frac{1}{2}$，则sin2α=（ ）
| A． | $±\frac{{\sqrt{3}}}{2}$ | B． | $±\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $-\frac{1}{2}$ |
7．已知点A（x0，y0）是抛物线y2=2px（p＞0）上一点，且它在第一象限内，焦点为F，O坐标原点，若|AF|=$\frac{3p}{2}$，|AO|=2$\sqrt{3}$，则此抛物线的准线方程为（ ）
| A． | x=-4 | B． | x=-3 | C． | x=-2 | D． | x=-1 |
4．设a，b∈R，函数f（x）=ax+b（0≤x≤1），则f（x）＞0恒成立是a+2b＞0成立的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 即不充分也不必要条件 |
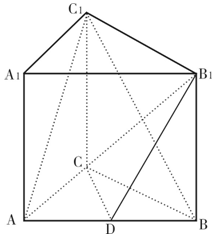如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=3，BC=4，AB=5，点D是AB的中点．