题目内容
18.“$cosα=\frac{1}{2}$”是“$α=\frac{π}{3}$”的( )| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 不充分也不必要条件 |
分析 根据充分条件和必要条件的定义进行判断即可.
解答 解:当$α=\frac{π}{3}$+2kπ时,满足$cosα=\frac{1}{2}$但$α=\frac{π}{3}$不一定成立,即充分性不成立,
当$α=\frac{π}{3}$时,$cosα=\frac{1}{2}$成立,即必要性成立,
则“$cosα=\frac{1}{2}$”是“$α=\frac{π}{3}$”的必要不充分条件,
故选:C
点评 本题主要考查充分条件和必要条件的判断,根据充分条件和必要条件的定义是解决本题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
13.集合A={x|y=ln(1-2x)},B={x|x2<x},全集U=A∪B,则∁U(A∩B)=( )
| A. | (-∞,0) | B. | $[\frac{1}{2},1]$ | C. | (-∞,0)∪$[\frac{1}{2},1]$ | D. | $(-\frac{1}{2},0]$ |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$与抛物线y2=2px(p>0)有公共焦点F且交于A,B两点,若直线AB过焦点F,则该双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |



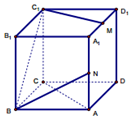 如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )