题目内容
已知等差数列{an}的各项都不为零,公差d>0,且a5+a10=0,记数列{-
}的前n项和为Sn,则使Sn<0成立的正整数n的最小值为 .
| 2 |
| an |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知条件推导出S14=0,S15<0,由此能求出使Sn<0成立的正整数n的最小值为15.
解答:
解:等差数列{an}的各项都不为零,公差d>0,
∵a5+a10=0,
∴a7+a8=0,a6+a9=0,a4+a11=0,a3+a12=0,a2+a13=0,a1+a14=0,
∴a1=-a14,a2=-a13,a3=-a12,a4=-a11,a5=-a10,a6=-a9,a7=-a8,
∴(-
)+(-
)=0,(-
)+(-
)=0,…,
∴S14=(-
)+(-
)+(-
)+…+(-
)=0,
∵a7=-a8,d>0,
∴a7<0,a8>0,则当n≤7时,an<0,当n≥8时,an>0,
∴当n≤7时,-
>0,当n≥8时,-
<0,
∴当n≤7时,Sn随着n的增大而增大,且大于0,当n≥8时,Sn随着n的增大而减小,
∴S15<0,
∴使Sn<0成立的正整数n的最小值为15.
故答案为:15.
∵a5+a10=0,
∴a7+a8=0,a6+a9=0,a4+a11=0,a3+a12=0,a2+a13=0,a1+a14=0,
∴a1=-a14,a2=-a13,a3=-a12,a4=-a11,a5=-a10,a6=-a9,a7=-a8,
∴(-
| 2 |
| a1 |
| 2 |
| a14 |
| 2 |
| a2 |
| 2 |
| a13 |
∴S14=(-
| 2 |
| a1 |
| 2 |
| a2 |
| 2 |
| a3 |
| 2 |
| a14 |
∵a7=-a8,d>0,
∴a7<0,a8>0,则当n≤7时,an<0,当n≥8时,an>0,
∴当n≤7时,-
| 2 |
| an |
| 2 |
| an |
∴当n≤7时,Sn随着n的增大而增大,且大于0,当n≥8时,Sn随着n的增大而减小,
∴S15<0,
∴使Sn<0成立的正整数n的最小值为15.
故答案为:15.
点评:本题考查使Sn<0成立的正整数n的最小值的求法,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
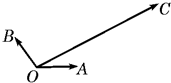 如图平面内有三个向量
如图平面内有三个向量