题目内容
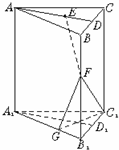
如图，已知直三棱柱ABC-A1B1C1，AB=AC，F为BB1上一点，D为BC的中点，且BF=2BD．（1）当
| BF |
| FB1 |
（2）若A1B1=3，C1F与平面AA1B1B所成角的正弦值为
4
| ||
| 15 |
| BF |
| FB1 |
考点：棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题：空间位置关系与距离
分析：（1）由已知条件推导出C1F⊥DF，Rt△BDF≌Rt△B1FC1，由此推导出
=2．
（2）在平面A1B1C1中，过C1作C1G⊥A1B1于G，连FG，则∠C1FG就是C1F与侧面AA1B1B所成的角，由此能求出三棱柱的体积．
| BF |
| B1F |
（2）在平面A1B1C1中，过C1作C1G⊥A1B1于G，连FG，则∠C1FG就是C1F与侧面AA1B1B所成的角，由此能求出三棱柱的体积．
解答：
（1）∵对于AD上任意一点总有EF⊥FC1，
∴C1F⊥平面ADF，
∴C1F⊥DF，
∵D为BC的中点，且BF=2BD，
∴BF=B1C1，∠B1FC1=∠BDF，∠FB1C1=∠DBF，
∴Rt△BDF≌Rt△B1FC1，
∴B1F=BD=
BF，∴
=2．（6分）
（2）在平面A1B1C1中，过C1作C1G⊥A1B1于G，连FG，
则∠C1FG就是C1F与侧面AA1B1B所成的角，（8分）
则有
=
，C1G=
C1F，
△A1B1C1中，取B1C1的中点D1，连A1D1，
设B1F=x，由C1G•A1B1=B1C1•A1D1，
解得x=1，∴BB1=3，（10分）
∴三棱柱的体积V=
B1G•A1D1•BB1=6
．（12分）
（1）∵对于AD上任意一点总有EF⊥FC1，∴C1F⊥平面ADF，
∴C1F⊥DF，
∵D为BC的中点，且BF=2BD，
∴BF=B1C1，∠B1FC1=∠BDF，∠FB1C1=∠DBF，
∴Rt△BDF≌Rt△B1FC1，
∴B1F=BD=
| 1 |
| 2 |
| BF |
| B1F |
（2）在平面A1B1C1中，过C1作C1G⊥A1B1于G，连FG，
则∠C1FG就是C1F与侧面AA1B1B所成的角，（8分）
则有
| C1G |
| C1F |
4
| ||
| 15 |
4
| ||
| 15 |
△A1B1C1中，取B1C1的中点D1，连A1D1，
设B1F=x，由C1G•A1B1=B1C1•A1D1，
解得x=1，∴BB1=3，（10分）
∴三棱柱的体积V=
| 1 |
| 2 |
| 2 |
点评：本题考查满足条件的线段的比值的求法，考查三飘棱锥的体积的求法，解题时要认真审题，注意空间思维能力的合理运用．
练习册系列答案
名题金卷系列答案
相关题目
已知映射f：A→B，其中集合A={-9，-3，-1，1，3，9}，集合B中的元素都是A中的元素在映射f下的象，且对于任意x∈A，在B中和它对应的元素是log3|x|，则集合B为（ ）
| A、{1，2，3} |
| B、{0，1，2} |
| C、{-2，-1，0，1，2} |
| D、{1，2} |
如图，平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ（不包含边界），设
| OP |
| OP1 |
| OP2 |
| A、m＞0，n＞0 |
| B、m＞0，n＜0 |
| C、m＜0，n＞0 |
| D、m＜0，n＜0 |
以下判断，正确的是（ ）
A、当0＜x＜2时，因为（2-x）（2-x）x≤（
| ||||
B、|sinθ+
| ||||
| C、若实数x，y，z满足xyz=1，则x+y+z的最小值为3 | ||||
| D、若?＞0，|x-a|＜?，|y+b|＜?，则|2x+y-2a+b|＜3? |