题目内容
以下判断,正确的是( )
A、当0<x<2时,因为(2-x)(2-x)x≤(
| ||||
B、|sinθ+
| ||||
| C、若实数x,y,z满足xyz=1,则x+y+z的最小值为3 | ||||
| D、若?>0,|x-a|<?,|y+b|<?,则|2x+y-2a+b|<3? |
考点:命题的真假判断与应用
专题:不等式的解法及应用,简易逻辑
分析:由利用基本不等式求最值的条件说明A错误;利用函数的单调性求出|sinθ+
|(θ≠kπ,k∈Z)的最小值说明B错误;举例说明C错误;由绝对值不等式的性质证明D正确.
| 2 |
| sinθ |
解答:
解:对于A,运用基本不等式求乘积最大值应满足和为定值,
而2-x+2-x+x不是定值.故选项A不正确;
对于B,θ≠kπ,k∈Z时,-1≤sinθ≤1且sinθ≠0.
由“对勾函数”的单调性可知,|sinθ+
|(θ≠kπ,k∈Z)的最小值为3.故选项B错误;
对于C,取x=-2,y=1,z=-
,满足xyz=1,但x+y+z的最小值为-
.故选项C错误;
对于D,若?>0,|x-a|<?,|y+b|<?,
则|2x+y-2a+b|=|2(x-a)+y+b|≤2|x-a|+|y+b|<3?.故选项D正确.
故选:D.
而2-x+2-x+x不是定值.故选项A不正确;
对于B,θ≠kπ,k∈Z时,-1≤sinθ≤1且sinθ≠0.
由“对勾函数”的单调性可知,|sinθ+
| 2 |
| sinθ |
对于C,取x=-2,y=1,z=-
| 1 |
| 2 |
| 3 |
| 2 |
对于D,若?>0,|x-a|<?,|y+b|<?,
则|2x+y-2a+b|=|2(x-a)+y+b|≤2|x-a|+|y+b|<3?.故选项D正确.
故选:D.
点评:本题考查了命题的真假判断与应用,考查了利用基本不等式求函数的最值,考查了绝对值不等式的性质,是中档题.

练习册系列答案
相关题目
已知平面上的非零向量
,
,
满足
+
+
=
,|
|=|
|=1,且cos<
,
>=-
,则△P1P2P3的形状为( )
| OP1 |
| OP2 |
| OP3 |
| OP1 |
| OP2 |
| OP3 |
| 0 |
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| 4 |
| 5 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
已知x1,x2分别是函数f(x)=log2x-(
)x和g(x)=log
x-(
)x的零点,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、x1x2<0 |
| B、0<x1x2<1 |
| C、x1x2=1 |
| D、1<x1x2<2 |
 如图,已知直三棱柱ABC-A1B1C1,AB=AC,F为BB1上一点,D为BC的中点,且BF=2BD.
如图,已知直三棱柱ABC-A1B1C1,AB=AC,F为BB1上一点,D为BC的中点,且BF=2BD.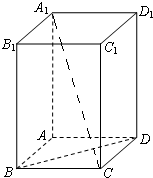 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接A1C,BD.