题目内容

已知点A（1，2），B（2，3），C（-2，5）．
（1）求证：
AB
⊥
AC
；
（2）若向量
a
=（1，-2）可表示为
a
=m
AB
+n
AC
，求实数m，n的值．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：（1）根据向量垂直的条件，求得
AB
•
AC
=0，问题得以解决．
（2）构建关于mn的方程组，解得即可．
解答： 解：（1）∵
AB
=(1，1)，
AC
=(-3，3)，
∴
AB
•
AC
=-3+3=0
∴
AB
⊥
AC
；
（2）∵
a
=m
AB
+n
AC
=m(1，1)+n(-3，3)=(m-3n，m+3n)
∴
m-3n=1
m+3n=-2

解得m=-
1
2
，n=-
1
2
点评：本题主要考查平面向量基本定理、两个向量坐标形式的运算以及向量的垂直的条件，属于基础题．
练习册系列答案
相关题目
函数f（x）=-x-1，则f（2x+3）=
 
．
已知x1，x2分别是函数f（x）=log2x-（
1
2
）x和g（x）=log
1
2
x-（
1
2
）x的零点，则（　　）
A、x1x2＜0
B、0＜x1x2＜1
C、x1x2=1
D、1＜x1x2＜2
如图，已知直三棱柱ABC-A1B1C1，AB=AC，F为BB1上一点，D为BC的中点，且BF=2BD．
（1）当
BF
FB1
为何值时，对于AD上任意一点总有EF⊥FC1；
（2）若A1B1=3，C1F与平面AA1B1B所成角的正弦值为
4
10
15
，当
BF
FB1
在（1）所给的值时，求三棱柱的体积．
已知函数f（x）=sin（π-x），x∈R．
（1）求函数f2（x）+cos2（π+x）的值；
（2）若f（α）=
3
5
，α∈[0，
π
2
]，求f（α-
π
6
）的值．
已知函数f（x）=cos2x+sinxcosx．
（Ⅰ）求f（x）的最小正周期和最小值；
（Ⅱ）若α∈（
π
4
，
π
2
）且f（α+
3π
8
）=
2-
6
4
，求α的值．
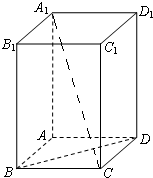如图所示，在长方体ABCD-A1B1C1D1中，AB=BC=1，BB1=2，连接A1C，BD．
（1）求三棱锥A1-BCD的体积．
（2）求证：A1C⊥BD．
如图，平行四边形ABCD中，E、F分别是BC，DC的中点，若
AB
=
a
，
AD
=
b
，试用
a
，
b
，表示
DE
、
BF
．
已知函数f（x）=lnx-ax+2在点（1，f（1））处的切线与直线l：x-y-1=0垂直，
（1）求实数a的值和函数f（x）的单调区间；
（2）若g（n）=1+
1
2
+
1
3
+…+
1
n
，h（n）=lnn，数列{an}：an=2g（n）-h（n），求实数m的取值范围，使对任意n∈N*，不等式an＞log2m-4logm2-1恒成立．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网