圆锥底面半径为r.母线长是底面半径的3倍.在底面圆周上有一点A.求一个动点P自A出发在侧面上绕一周到A点的最短路程．题目和参考答案——青夏教育精英家教网—

题目内容

圆锥底面半径为r，母线长是底面半径的3倍，在底面圆周上有一点A，求一个动点P自A出发在侧面上绕一周到A点的最短路程．

考点：多面体和旋转体表面上的最短距离问题

专题：计算题,三角函数的求值

分析：圆锥的侧面展开图是扇形，从A点出发绕侧面一周，再回到A点的最短的路线即展开得到的扇形的弧所对弦，转化为求弦长的问题．

解答：

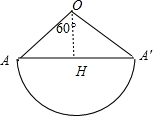解：∵圆锥底面半径为r，母线长是底面半径的3倍，
∴根据弧长公式得到2πr=α•3r，
∴α=

2π

，即扇形的圆心角是

2π

，
∴动点P自A出发在侧面上绕一周到A点的最短路程为弧所对的弦长AA′=2×3sin60°=3

．

点评：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把圆锥的侧面展开成扇形，“化曲面为平面”，用勾股定理解决．

练习册系列答案

相关题目

．
①“a＞b”是“a²＞b²”的充分条件；
②“|a|＞|b|”是“a²＞b²”的必要条件；
③“a＞b”是“a+c＞b+c”的充要条件．

已知x+y+4＞3x+y-2＞0，若x-y＜λ恒成立，则λ取值范围是（　　）

共线的充要条件；
②空间任意一点O与不共线三点A，B，C满足

-4

，则P，A，B，C四点共面；
③若两平面的法向量不垂直，则这两个平面一定不垂直．
其中正确的命题是（　　）

给出如下四个命题：
①若“p∧q”为假命题，则p，q均为假命题；
②命题“若a＞b，则2^a＞2^b-1”的否命题为“若a≤b，则2^a≤2^b-1”；
③“?x∈R，x²+1≥1”的否定是“?x₀∈R，x₀²+1≤1”
④给出四个函数y=x^-1，y=x，y=x²，y=x³，则在R上是增函数的有3个．
其中不正确的命题个数是（　　）

甲乙丙丁4人玩传球游戏，持球者将球等可能的传给其他3人，若球首先从甲传出，经过3次传球．
（1）求球恰好回到甲手中的概率；
（2）设乙获球（获得其他游戏者传的球）的次数为ξ，求ξ的分布列及数学期望．

已知函数f（x）=x²+xsinx+cosx．
（1）求f（x）的最小值；
（2）若曲线y=f（x）在点（a，f（a））处与直线y=b相切，求a与b的值．
（3）若曲线y=f（x）与直线y=b 有两个不同的交点，求b的取值范围．

已知函数f（x）=x-

-lnx，a＞0．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）若f（x）＞x-x²在（1，+∞）恒成立，求实数a的取值范围．

有下列说法：
①S_n是数列{a_n}的前n项和，若S_n=n²+n+1，则数列{a_n}是等差数列；
②若实数x，y满足x²+y²=4，则

x+y-2

的最小值是1-

；
③在△ABC中，a，b，c分别是角A、B、C的对边，若acosA=bcosB，则△ABC 为等腰直角三角形；
④△ABC中，“A＞B”是“sinA＞sinB”的充要条件．
其中正确的有

．（填上所有正确命题的序号）

试题分类