题目内容
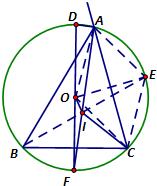如图，设O，I分别为△ABC的外心、内心，且∠B=60°，AB＞BC，∠A的外角平分线交⊙O于D，已知AD=18，则OI=．考点：与圆有关的比例线段
专题：直线与圆
分析：连接BI并延长交⊙O于E，连结OE、AE、CE、OC，由已知条件推导出A、O、I、C四点共圆，且圆心为E．再延长AI交⊙O于F，推导出△OAD≌△EOI，由此能求出OI的长．
解答：
解：连接BI并延长交⊙O于E，则E为弧AC的中点．
连结OE、AE、CE、OC，
∵∠B=60°，∴△AOE、△COE均为正三角形．
由内心的性质得知：AE=IE=CE，
∴A、O、I、C四点共圆，且圆心为E．
再延长AI交⊙O于F，
由题设知D、O、F共线，
∴∠OEI2∠OAI，∠AOD=2∠AFD=2∠OAI，
又∵OA=OD=OE=IE，
∴△OAD≌△EOI，
∴OI=AD=18．
故答案为：18．
连结OE、AE、CE、OC，
∵∠B=60°，∴△AOE、△COE均为正三角形．
由内心的性质得知：AE=IE=CE，
∴A、O、I、C四点共圆，且圆心为E．
再延长AI交⊙O于F，
由题设知D、O、F共线，
∴∠OEI2∠OAI，∠AOD=2∠AFD=2∠OAI，
又∵OA=OD=OE=IE，
∴△OAD≌△EOI，
∴OI=AD=18．
故答案为：18．
点评：本题考查与圆有关的线段长的求法，是中档题，解题时要认真审题，注意圆的性质的灵活运用．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
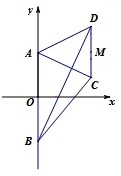如图，梯形ABCD的底边AB在y轴上，原点O为AB的中点，|AB|=