题目内容
已知函数f(x)=5|x|,g(x)=ax2-x(a∈R),若f[g(1)]=1,则a= .
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:先求出g(1)=a-1,再代入f[g(1)]=1,得到|a-1|=0,问题得以解决.
解答:
解:∵f(x)=5|x|,g(x)=ax2-x(a∈R),f[g(1)]=1,
∴g(1)=a-1,
∴f[g(1)]=f(a-1)=5|a-1|=1=50,
∴|a-1|=0,
∴a=1,
故答案为:1.
∴g(1)=a-1,
∴f[g(1)]=f(a-1)=5|a-1|=1=50,
∴|a-1|=0,
∴a=1,
故答案为:1.
点评:本题主要考查了指数的性质,和函数值得求出,属于基础题.

练习册系列答案
相关题目
已知方程
=k在(0,+∞)上有两个不同的解a,b(a<b),则下面结论正确的是( )
|cos(x-
| ||
| x |
| A、sina=acosb |
| B、sina=-acosb |
| C、cosa=bsinb |
| D、sinb=-bsina |
设f(x),g(x)都是定义在R上的奇函数,且F(x)=3f(x)+5g(x)+2,若F(a)=b则F(-a)等于( )
| A、-b+4 | B、-b+2 |
| C、b-2 | D、b+2 |
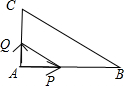 在△ABC中,∠B=30°,∠C=60°,AC=1,动点P,Q同时从A出发,沿周界运动,点P沿A→B→C;动点Q沿A→C→B运动到相遇时停止,动点Q的速度是动点P的运动速度的3倍,AP=x,△APQ的面积为y,求函数y=f(x)的解析式,并确定PQ在什么位置时S最大.
在△ABC中,∠B=30°,∠C=60°,AC=1,动点P,Q同时从A出发,沿周界运动,点P沿A→B→C;动点Q沿A→C→B运动到相遇时停止,动点Q的速度是动点P的运动速度的3倍,AP=x,△APQ的面积为y,求函数y=f(x)的解析式,并确定PQ在什么位置时S最大.