Question

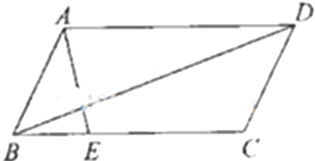
已知平行四边形ABCD中，AB=1，E是BC边上靠近点B的三等分点，AE⊥BD，则BC长度的取值范围是

 

．

Answer 1

考点：直线的一般式方程与直线的垂直关系

专题：直线与圆

分析：建立坐标系，利用AB=1，AE⊥BD，可得

a2+b2

=1，k_BD•k_AE=

b

a+c

×

b

a- c 3

=-1，化简整理即可得出．

解答： 解：如图所示，建立直角坐标系．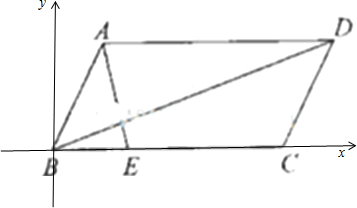
设A（a，b），C（c，0），则E(

c

3

，0)，D（a+c，b）．
∵AB=1，AE⊥BD，
∴

a2+b2

=1，
k_BD•k_AE=

b

a+c

×

b

a- c 3

=-1，
化为a²+b²=1，b2+a2+

2

3

ac-

1

3

c2=0．
∴1+

2

3

ac-

1

3

c2=0，
∴a=

c2-3

2c

，
∵0＜a＜1，
∴0＜

c2-3

2c

＜1，c＞0．
解得

3

＜c＜3．
故答案为：（

3

，3）．

点评：本题考查了两点之间的距离公式、相互垂直的直线斜率之间的关系，考查了计算能力，属于中档题．