题目内容
f（x）=sin2x+cosx，求f（x）的值域．
考点：三角函数的最值
专题：函数的性质及应用
分析：先利用同角三角函数基本关系转化函数解析式，利用换元法把问题转换为一元二次函数，求其最大和最小值．
解答：
解：f（x）=sin2x+cosx=-cos2x+cosx+1，
令cosx=t，t∈[-1，1]，
f（x）=f（t）=-t2+t+1=-（t-
）2+
，
∴f（x）max=f（
）=
，
f（x）min=f（-1）=-1，
∴函数的值域为[-1，
]
令cosx=t，t∈[-1，1]，
f（x）=f（t）=-t2+t+1=-（t-
| 1 |
| 2 |
| 5 |
| 4 |
∴f（x）max=f（
| 1 |
| 2 |
| 5 |
| 4 |
f（x）min=f（-1）=-1，
∴函数的值域为[-1，
| 5 |
| 4 |
点评：本题主要考查了二次函数的图象和性质．注重了换元法，转换和化归思想的运用．
练习册系列答案
相关题目
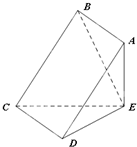如图，E是平面ABCD外一点，AE⊥平面CDE．若四边形ABCD是正方形，M，N分别是AE，BC的中点．