题目内容
为了了解某次考试A,B两个班的数学成绩的情况,现分别从A,B班各抽取20位同学的数学成绩(满分100分)进行研究,得到茎叶图如图所示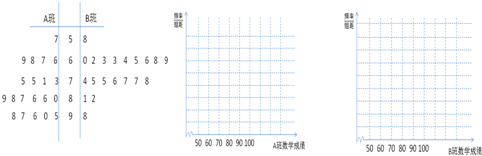
(1)比较A,B两个班的数学成绩的平均水平和差异程度(不用计算,通过观察茎叶图直接回答结论)
(2)现将A,B班的学生成绩按[50,60),[60,70)[70,80),[80,90),[90,100]分成5组,分别列出频率分布表并完成频率分布直方图.

(1)比较A,B两个班的数学成绩的平均水平和差异程度(不用计算,通过观察茎叶图直接回答结论)
(2)现将A,B班的学生成绩按[50,60),[60,70)[70,80),[80,90),[90,100]分成5组,分别列出频率分布表并完成频率分布直方图.
考点:茎叶图,频率分布直方图,极差、方差与标准差
专题:概率与统计
分析:(1)分析图中两组数据的叶峰位置及数据集中程度,可得到A,B两个班的数学成绩的平均水平和差异程度;
(2)分别求出各组的频率,频率及对应矩形的高,可画出频率分布直方图.
(2)分别求出各组的频率,频率及对应矩形的高,可画出频率分布直方图.
解答:
解:(1)∵茎叶图中,A班数据的叶峰靠下,
故A班的数学平均成绩要高于B班的数学平均成绩,
但B班的数据更集中,
故B班的数学成绩差异度要小.
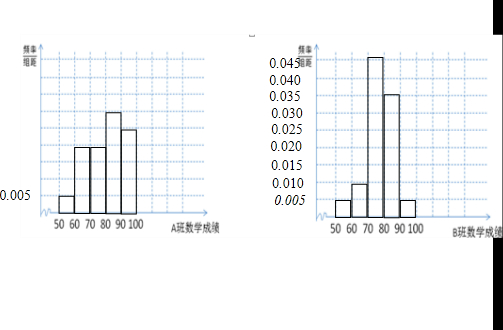
(2)A、B班数学成绩的频率分布表和频率分布直方图如下:
A、B班数学成绩的频率分布直方图,如下图所示:
故A班的数学平均成绩要高于B班的数学平均成绩,
但B班的数据更集中,
故B班的数学成绩差异度要小.
(2)A、B班数学成绩的频率分布表和频率分布直方图如下:
| 分组A班 | 频数 | 频率 | 频率/组距 |
| [50,60) | 1 | 0.05 | 0.005 |
| [60,70) | 4 | 0.2 | 0.02 |
| [70,80) | 4 | 0.2 | 0.02 |
| [80,90) | 6 | 0.3 | 0.03 |
| [90,100] | 5 | 0.25 | 0.025 |
| 分组B班 | 频数 | 频率 | 频率/组距 |
| [50,60) | 1 | 0.05 | 0.005 |
| [60,70) | 9 | 0.45 | 0.045 |
| [70,80) | 7 | 0.35 | 0.035 |
| [80,90) | 2 | 0.10 | 0.010 |
| [90,100] | 1 | 0.05 | 0.005 |

点评:本题考查的知识点是茎叶图及应用,频率分布直方图,难度不大,属于基础题.

练习册系列答案
相关题目
 如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点.
如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点. 已知点F是抛物线Γ:x2=2py(p>0)的焦点,点M(x0,1)到F的距离为2.
已知点F是抛物线Γ:x2=2py(p>0)的焦点,点M(x0,1)到F的距离为2.