题目内容
在平面直角坐标系xOy中,直线l的参数方程为
(参数t∈R),圆C的参数方程为
(参数θ∈[0,2π]),则圆C的圆心坐标为 ,圆心到直线l的距离为 .
|
|
考点:直线的参数方程,圆的参数方程
专题:选作题,坐标系和参数方程
分析:先利用两式相加消去t将直线的参数方程化成普通方程,然后利用sin2θ+cos2θ=1将圆的参数方程化成圆的普通方程,求出圆心和半径,最后利用点到直线的距离公式求出圆心到直线的距离即可.
解答:
解:直线l的参数方程为
(参数t∈R),
∴直线的普通方程为x+y-6=0;
圆C的参数方程为
(参数θ∈[0,2π]),
∴圆C的普通方程为x2+(y-2)2=4
∴圆C的圆心为(0,2),d=2
.
故答案为:(0,2);2
.
|
∴直线的普通方程为x+y-6=0;
圆C的参数方程为
|
∴圆C的普通方程为x2+(y-2)2=4
∴圆C的圆心为(0,2),d=2
| 2 |
故答案为:(0,2);2
| 2 |
点评:本小题主要考查圆的参数方程及直线与圆的位置关系的判断,以及转化与化归的思想方法.本题出现最多的问题应该是计算上的问题,平时要强化基本功的练习,属于基础题.

练习册系列答案
相关题目
 一次期末考试,学校随机抽取了一批学生的物理成绩(满分100分),经统计,这批抽取的学生的成绩全部介于65分到100分之间,现将数据分成以下7组:第1组[65,70],第2组[70,75],第3组[75,80],第4组[80.85],第5组[85,90],第6组[90,95],第7组[95,100],得到如图所示的频率分布直方图(不完整).
一次期末考试,学校随机抽取了一批学生的物理成绩(满分100分),经统计,这批抽取的学生的成绩全部介于65分到100分之间,现将数据分成以下7组:第1组[65,70],第2组[70,75],第3组[75,80],第4组[80.85],第5组[85,90],第6组[90,95],第7组[95,100],得到如图所示的频率分布直方图(不完整).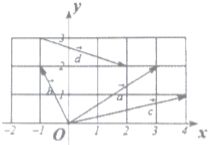 如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底.
如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底. 如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点.
如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点.