题目内容
已知函数f(x)=lnx-
ax2+(a-1)x.
(Ⅰ)当a=2时,求函数f(x)的单调递增区间;
(Ⅱ)当a>0时,试确定函数y=
a2-f(x)的零点个数,并说明理由.
| 1 |
| 2 |
(Ⅰ)当a=2时,求函数f(x)的单调递增区间;
(Ⅱ)当a>0时,试确定函数y=
| 1 |
| 4 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(Ⅰ)在定义域内解不等式f′(x)>0即可;
(Ⅱ)令g(x)=
a2-f(x)=
a2-lnx+
ax2-(a-1)x,利用导数可求得g(x)唯一的极小值,且判断极小值大于0,由此可得结论;
(Ⅱ)令g(x)=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
解答:
解:(Ⅰ)显然函数f(x)的定义域是(0,+∞),
由已知得f(x)=lnx-
ax2+(a-1)x=lnx-x2+x,
f′(x)=
-2x+1=
=-
,
令f′(x)>0,解得-
<x<1,函数的定义域是(0,+∞),
∴函数f(x)的单调递增区间是(0,1).
(Ⅱ)令g(x)=
a2-f(x)=
a2-lnx+
ax2-(a-1)x,
则g′(x)=-
+ax-(a-1)=
,
∵a>0,∴ax+1>0,
当x∈(0,1)时,g′(x)<0,g(x)递减;当x∈(1,+∞)时,g′(x)>0g(x)递增.
∴g(x)min=g(1)=
a2+
a-(a-1)=
(a-1)2+
>0,
故g(x)的零点个数为0个.
由已知得f(x)=lnx-
| 1 |
| 2 |
f′(x)=
| 1 |
| x |
| 1-2x2+x |
| x |
| (x-1)(2x+1) |
| x |
令f′(x)>0,解得-
| 1 |
| 2 |
∴函数f(x)的单调递增区间是(0,1).
(Ⅱ)令g(x)=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
则g′(x)=-
| 1 |
| x |
| (ax+1)(x-1) |
| x |
∵a>0,∴ax+1>0,
当x∈(0,1)时,g′(x)<0,g(x)递减;当x∈(1,+∞)时,g′(x)>0g(x)递增.
∴g(x)min=g(1)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
故g(x)的零点个数为0个.
点评:该题考查利用导数研究函数的单调性、极值、零点个数问题,考查学生分析解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=(x+2)2(x-1)3的极大值点是( )
| A、x=-2或1 |
| B、x=-1或2 |
| C、x=-1 |
| D、x=-2 |
 已知圆锥的侧面展开图是圆心角为120°的扇形,且圆锥的全面积为
已知圆锥的侧面展开图是圆心角为120°的扇形,且圆锥的全面积为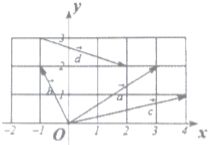 如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底.
如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底.