题目内容
8.为了解某班学生喜欢打篮球是否与性别有关,对本班50人进行了问卷调查,得到如下2×2列联表:| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥K0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 根据随机变量K2的观测值,对照临界值表即可得出结论.
解答 解:根据表中数据计算得到随机变量K2的观测值为8.333,
对照临界值表知8.333>7.879,
∴有99.5%的把握认为喜爱打篮球与性别有关.
点评 本题考查了独立性检验的应用问题,是基础题.

练习册系列答案
相关题目
18.已知在△ABC中,角A,B,C所对的边分别为a,b,c,若C=2A,c=$\sqrt{3}$a,则$\frac{b}{a}$等于( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 1或2 |
3.已知数列{an}为等比数列,若a2=2,a10=8,则a6=( )
| A. | ±4 | B. | -4 | C. | 4 | D. | 5 |
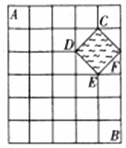 如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.
如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.