题目内容
已知正三棱锥S-ABC的所有棱长均为2,则侧面与底面所成二面角的余弦为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:二面角的平面角及求法
专题:计算题,空间角
分析:利用正三棱锥的性质和二面角的定义、等边三角形的性质即可求出.
解答:
解:如图所示,过点S作SO⊥底面ABC,点O为垂足,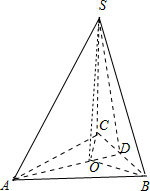
连接OA、OB、OC,则Rt△OAB≌Rt△OBC≌Rt△OCA,∴OA=OB=OC,
∴点O为等边△ABC的中心.
延长AO交BC于点D,连接SD.
则AD⊥BC,再根据三垂线定理可得BC⊥SD.
∴∠ODS为侧面SBC与底面ABC所成的二面角的平面角.
根据重心定理可得:OD=
AD=
.
在Rt△SOD中,cos∠ODS=
=
,
故选C.

连接OA、OB、OC,则Rt△OAB≌Rt△OBC≌Rt△OCA,∴OA=OB=OC,
∴点O为等边△ABC的中心.
延长AO交BC于点D,连接SD.
则AD⊥BC,再根据三垂线定理可得BC⊥SD.
∴∠ODS为侧面SBC与底面ABC所成的二面角的平面角.
根据重心定理可得:OD=
| 1 |
| 3 |
| ||
| 3 |
在Rt△SOD中,cos∠ODS=
| SO |
| OD |
| 1 |
| 3 |
故选C.
点评:熟练掌握正三棱锥的性质和二面角的定义、等边三角形的性质是解题的关键.

练习册系列答案
相关题目
由曲线y=
与直线x=1,及x=4围成的图形的面积等于( )
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
一只蚂蚁从长方体ABCD-A1B1C1D1的顶点A出发,沿着长方体的表面到达顶点C1的最短距离为6,则长方体体积的最大值为( )
| A、24 | ||
B、6
| ||
C、12
| ||
D、9
|
函数f(x)=|lgx|-(
)x的零点个数为( )
| 1 |
| 2 |
| A、3 | B、0 | C、1 | D、2 |
双曲线
-
=1(a>0,b>0)的两条渐近线与抛物线y=x2+1有四个公共点,则该双曲线的离心率的取值范围是( )
| y2 |
| a2 |
| x2 |
| b2 |
A、(1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(
|
如果25,x,y,z,1成等比数列,那么( )
| A、y=5,xz=25 |
| B、y=-5,xz=25 |
| C、y=5,xz=-25 |
| D、y=-5,xz=-25 |