题目内容
球的内接正方体的体积与球的体积之比为 .
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:设出正方体的棱长,求出正方体的体对角线的长,就是球的直径,然后求出正方体的体积,球的体积,即可得到比值.
解答:
解:设正方体的棱长为:1,则正方体的体对角线的长为:
,所以正方体的外接球的直径为:
所以正方体的体积为:1;球的体积为:
•(
)3=
所以球的内接正方体的体积与球的体积之比为2:
π.
故答案为:2:
π.
| 3 |
| 3 |
所以正方体的体积为:1;球的体积为:
| 4π |
| 3 |
| ||
| 2 |
| ||
| 2 |
所以球的内接正方体的体积与球的体积之比为2:
| 3 |
故答案为:2:
| 3 |
点评:本题考查球的体积,球的内接体知识,找出二者的关系,球的直径就是正方体的体对角线,是本题解题的关键,考查计算能力,是基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
在一个装满水的容积为1升的容器中有两个相互独立、自由游弋的草履虫,现在从这个容器中随机取出0.1升水,则在取出的水中发现草履虫的概率为( )
| A、0.10 | B、0.09 |
| C、0.19 | D、0.199 |
函数f(x)=
-2sinπx在区间[-2,4]上的所有零点之和等于( )
| 1 |
| 1-x |
| A、2 | B、6 | C、8 | D、10 |
已知正三棱锥S-ABC的所有棱长均为2,则侧面与底面所成二面角的余弦为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
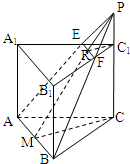 已知正三棱柱ABC-A1B1C1底面边长是10,高是12,过底面一边AB,作与底面ABC成60°角的截面面积是
已知正三棱柱ABC-A1B1C1底面边长是10,高是12,过底面一边AB,作与底面ABC成60°角的截面面积是 正三角形ABC,点M,N,P分别为AB,BC,AC中点,沿MN,MP,NP折起,使A,B,C三点重合后为Q,则折起后二面角Q-MN-P的余弦值为
正三角形ABC,点M,N,P分别为AB,BC,AC中点,沿MN,MP,NP折起,使A,B,C三点重合后为Q,则折起后二面角Q-MN-P的余弦值为