题目内容
关于f(x)=3sin(2x+
)有以下命题,其中正确命题的个数( )
①若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z);
②f(x)图象与g(x)=3cos(2x-
)图象相同;
③f(x)在区间[-
,-
]上是减函数;
④f(x)图象关于点(-
,0)对称.
| π |
| 4 |
①若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z);
②f(x)图象与g(x)=3cos(2x-
| π |
| 4 |
③f(x)在区间[-
| 7π |
| 8 |
| 3π |
| 8 |
④f(x)图象关于点(-
| π |
| 8 |
| A、0 | B、1 | C、2 | D、3 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:考查f(x)=3sin(2x+
)的零点、周期性、对称性、单调性,可得结论.
| π |
| 4 |
解答:
解:关于f(x)=3sin(2x+
),由于它的周期为π,相邻的两个零点相差半个周期,
故若f(x1)=f(x2)=0,则x1-x2=k•
(k∈Z),故①不正确.
由于g(x)=3cos(2x-
)=3sin(2x-
+
)=f(x)=3sin(2x+
),故②正确.
由2kπ+
≤2x+
≤2kπ+
,k∈z,求得 kπ+
≤x≤kπ+
,
故函数f(x)的减区间为[kπ+
≤x≤kπ+
],k∈z,故f(x)在区间[-
,-
]上是减函数,
故③正确.
把x=-
代入f(x)的解析式求得f(x)=0,可得f(x)图象关于点(-
,0)对称,故④正确.
故选:D.
| π |
| 4 |
故若f(x1)=f(x2)=0,则x1-x2=k•
| π |
| 2 |
由于g(x)=3cos(2x-
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
由2kπ+
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
故函数f(x)的减区间为[kπ+
| π |
| 8 |
| 5π |
| 8 |
| 7π |
| 8 |
| 3π |
| 8 |
故③正确.
把x=-
| π |
| 8 |
| π |
| 8 |
故选:D.
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的零点、周期性、对称性、单调性,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
函数f(x)=
-2sinπx在区间[-2,4]上的所有零点之和等于( )
| 1 |
| 1-x |
| A、2 | B、6 | C、8 | D、10 |
已知正三棱锥S-ABC的所有棱长均为2,则侧面与底面所成二面角的余弦为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列给出的赋值语句中,正确的是( )
| A、3=A | B、M=-3*M |
| C、B=A=2 | D、x+y=0 |
若变量x,y满足约束条件
,则z=
取得的最大值是( )
|
| y+3 |
| x+2 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
已知不等式组
,表示的三角形区域为M,过该区域三顶点的圆内部记为N,在N中随机取一点,则该点取自区域M的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若点P(x,y)在椭圆
+
=1上,则x的范围是( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、[-4,4] | ||||
| B、[-2,2] | ||||
| C、[-3,3] | ||||
D、[-
|
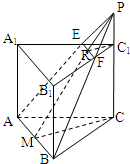 已知正三棱柱ABC-A1B1C1底面边长是10,高是12,过底面一边AB,作与底面ABC成60°角的截面面积是
已知正三棱柱ABC-A1B1C1底面边长是10,高是12,过底面一边AB,作与底面ABC成60°角的截面面积是