题目内容
设函数f（x）=
在区间（a，a+2）上单调递增，则a的取值范围为 ．
| lnx |
| x |
考点：利用导数研究函数的单调性,函数单调性的性质
专题：导数的综合应用
分析：求出函数的导数，利用函数单调性的和导数之间的关系即可得到结论．
解答：
解：∵f（x）=
的定义域为（0，+∞），
∴f′（x）=
，
由f′（x）=
＞0，解得0＜x＜e，
即函数的递增区间为（0，e），
若函数f（x）在区间（a，a+2）上单调递增，
则
，
即0≤a≤e-2，
故答案为：[0，e-2]
| lnx |
| x |
∴f′（x）=
| 1-lnx |
| x2 |
由f′（x）=
| 1-lnx |
| x2 |
即函数的递增区间为（0，e），
若函数f（x）在区间（a，a+2）上单调递增，
则
|
即0≤a≤e-2，
故答案为：[0，e-2]
点评：本题主要考查函数单调性和导致的关系，求出函数的单调区间是解决本题的关键．
练习册系列答案
相关题目
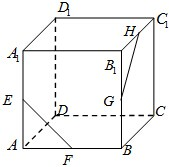如图，在正方体ABCDA1B1C1D1中，E、F、G、H分别为AA1、AB、BB1、BC1的中点，则异面直线EF与GH所成的角等于（ ）| A、30° | B、45° |
| C、60° | D、90° |
设f（x）=
，则
f（x）dx的值为（ ）
|
| ∫ | 2 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|