题目内容
若动点A(x1,y1)、B(x2,y2)分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,设AB中点M的坐标为(x0,y0),满足y0>x0+8,则
的取值范围是 .
| y0 |
| x0 |
考点:直线的斜率
专题:直线与圆
分析:如图所示,由于动点A(x1,y1)、B(x2,y2)分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,又AB中点Mx0,y0),满足y0>x0+8,可知:点M在直线y=x+8的左上方,且在直线y=-x+6上.再利用斜率的计算公式及其意义即可得出.
解答:
解:如图所示,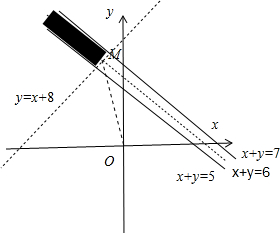
动点A(x1,y1)、B(x2,y2)分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,
又AB中点Mx0,y0),满足y0>x0+8,
∴点M在直线y=x+8的左上方,且在直线y=-x+6上.
联立
,解得
,此时kOM=
=-7.
则0>
>-7.
∴
的取值范围是(-7,0).
故答案为:(-7,0).

动点A(x1,y1)、B(x2,y2)分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,
又AB中点Mx0,y0),满足y0>x0+8,
∴点M在直线y=x+8的左上方,且在直线y=-x+6上.
联立
|
|
| 7 |
| -1 |
则0>
| y0 |
| x0 |
∴
| y0 |
| x0 |
故答案为:(-7,0).
点评:本题考查了线性规划的有关知识、斜率的计算公式及其意义、中点坐标公式,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
函数y=tan2x的最小正周期是( )
| A、π | ||
B、
| ||
C、
| ||
| D、2π |