题目内容
一支田径运动队有男运动员56人，女运动员42人．现用分层抽样的方法抽取若干人，若抽取的男运动员有8人，则抽取的女运动员人数为（ ）
| A、12 | B、10 | C、8 | D、6 |
考点：分层抽样方法
专题：概率与统计
分析：设抽取的女运动员人数为x，根据在分层抽样中，在各部分抽取的比例相等求得x．
解答：
解：设抽取的女运动员人数为x，
∵在分层抽样中，抽取的比例相等，
∴
=
⇒x=6．
故选：D．
∵在分层抽样中，抽取的比例相等，
∴
| 8 |
| 56 |
| x |
| 42 |
故选：D．
点评：本题考查了分层抽样方法，熟练掌握分层抽样的特征是解题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
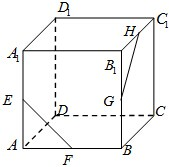如图，在正方体ABCDA1B1C1D1中，E、F、G、H分别为AA1、AB、BB1、BC1的中点，则异面直线EF与GH所成的角等于（ ）| A、30° | B、45° |
| C、60° | D、90° |
在△ABC中，已知sinB=2sin（B+C）cosC，那么△ABC一定是（ ）
| A、等腰直角三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等边三角形 |
函数y=tan2x的最小正周期是（ ）
| A、π | ||
B、
| ||
C、
| ||
| D、2π |
点S，A，B，C是球O的球面上的四个点，S，O在平面ABC的同侧，∠ABC=120°，AB=BC=2，平面SAC⊥平面ABC，若三棱锥S-ABC的体积为
，则该球的表面积为（ ）
| 3 |
| A、18π | B、16π |
| C、20π | D、25π |
设f（x）=
，则
f（x）dx的值为（ ）
|
| ∫ | 2 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知定义域为R的奇函数f（x）的导函数为f′（x），当x≠0时，f′（x）+
＞0，若a=
f（
），b=-2f（-2），c=ln
f（ln2），则下列关于a，b，c的大小关系正确的是（ ）
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞b＞a |
| D、a＞c＞b |
已知g（x）=ax+2，f（x）=
，对?x1∈[-1，3]，?x0∈[-1，3]，使g（x1）=f（x0）恒成立，则a的取值范围是（ ）
|
| A、a≥-1 | ||
B、-1≤a≤
| ||
C、0＜a≤
| ||
D、a≤
|