题目内容

已知向量 
a
=（sinx，
3
cosx），
b
=（cosx，cosx），若函数f（x）=
a
•
b

（Ⅰ） 若
a
⊥
b
，求x的值；
（Ⅱ） 求函数f（x）的递增区间．
考点：平面向量数量积的运算,三角函数中的恒等变换应用
专题：平面向量及应用
分析：（I）由
a
⊥
b
，可得
a
•
b
=sin(2x+
π
3
)+
3
2
=0．再利用正弦函数的单调性与周期性即可得出．
（II）由2kπ-
π
2
≤2x+
π
3
≤2kπ+
π
2
，解得 kπ-
5π
12
≤x≤kπ+
π
12
，k∈Z．即可得出．
解答： 解：（I）∵
a
⊥
b
，
∴
a
•
b
=sinxcosx+
3
cos2x=
1
2
sin2x+
3
(1+cos2x)
2
=sin(2x+
π
3
)+
3
2
=0．
∴sin(2x+
π
3
)=-
3
2
，
∴2x+
π
3
=kπ-(-1)k•
π
3
，解得x=
kπ
2
+(-1)k+1•
π
3
-
π
6
，k∈Z．
∴x∈{x|x=
kπ
2
+(-1)k+1•
π
3
-
π
6
，k∈Z}．
（II）由2kπ-
π
2
≤2x+
π
3
≤2kπ+
π
2
，解得 kπ-
5π
12
≤x≤kπ+
π
12
，k∈Z．
∴函数f（x）的递增区间是[kπ-
5π
12
，kπ+
π
12
]，k∈Z．
点评：本题考查了数量积运算、两角和差的正弦公式、倍角公式、正弦函数的单调性与周期性，考查了计算能力，属于中档题．
练习册系列答案
相关题目
要从A、B、C、D、E、F这6人中选出4人参加4×100m的接力赛；
（1）不同的参赛方式有几种；
（2）若A、B均参加且A必须跑第一棒，不同的参赛方式有几种．
已知函数f（x）=ex-tx（e为自然对数的底数）．
（1）求函数f（x）的单调增区间；
（2）设关于x的不等式f（x）≥x2-2t-3的解集为M，且集合{x|x≥3}⊆M，求实数t的取值范围．
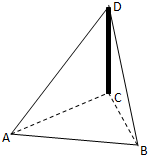如图所示，哈三中甲，乙两位同学分别站在新校区体育场内的A，B两点，利用三角函数知识测量锅炉房烟囱CD的高．已知AB=15米，∠DAC=60°，∠CAB=15°，∠CBA=45°，求烟囱CD的高．
直线l：
x=a+4t
y=-1-2t
（t为参数），圆C：ρ=2
2
cos（θ+
π
4
）（极轴与x轴的非负半轴重合，且单位长度相同），若直线l被圆C截得的弦长为
6
5
5
，求实数a的值．
已知平面向量
a
=（cosx，sinx），
b
=（2sinx，-2cosx），
c
=
a
+m
b
，
d
=cos2x•
a
+sinx•
b
，f（x）=
c
•
d
，x∈R．
（1）当m=2时，求y=f（x）的取值范围；
（2）若f（x）的最大值是7，求实数m的值；
（3）（仅理科同学做，文科同学不做）若f（x）的最大值是g（m），对任意的m∈R，都有g（m）≥km-3恒成立，求实数k的取值范围．
已知函数f（x）=
a
3
x3-
3
2
x2+（a+1）x+1，其中a为实数；
（1）当a=1时，试讨论函数g（x）=f（x）-m的零点的个数；
（2）已知不等式f'（x）＞x2-x-a+1对任意a∈（0，+∞）都成立，求实数x的取值范围．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点为F1、F2，点P在椭圆C上，且|PF1|=
4
3
，
|PF2|=
14
3
，PF1⊥F1F2．
（1）求椭圆C的方程；
（2）若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点，且A、B关于点M对称，求直线L的方程．
已知四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD是正方形，且PD=AB=2．
（1）求PB的长；
（2）求证：AC⊥平面PBD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网