题目内容
11.已知椭圆C1与双曲线C2具有相同的焦点F1,F2,A为C1与C2的一个公共点,△AF1F2为等腰三角形,设椭圆C1与双曲线C2的离心率分别为e1,e2,则( )| A. | e1e2=1 | B. | e1e2=2 | C. | e1+e2=2 | D. | $\frac{1}{{e}_{1}}$+$\frac{1}{{e}_{2}}$=2 |
分析 由题意画出图象,设椭圆与双曲线的标准方程分别为:$\frac{{x}^{2}}{{{a}_{1}}^{2}}+\frac{{y}^{2}}{{{b}_{1}}^{2}}=1$和$\frac{{x}^{2}}{{{a}_{2}}^{2}}-\frac{{y}^{2}}{{{b}_{2}}^{2}}=1$,根据图象和条件、椭圆和双曲线的定义列出方程,化简后根据离心率公式变形即可得到答案.
解答 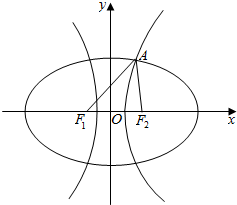 解:由题意画出图象:
解:由题意画出图象:
设椭圆与双曲线的标准方程分别为:$\frac{{x}^{2}}{{{a}_{1}}^{2}}+\frac{{y}^{2}}{{{b}_{1}}^{2}}=1$和$\frac{{x}^{2}}{{{a}_{2}}^{2}}-\frac{{y}^{2}}{{{b}_{2}}^{2}}=1$,
(a1,a2,b1,b2>0,a1>b1),
由图可得,|AF1|>|AF2|,
因为△AF1F2的等腰三角形,所以由图可得|AF1|=|F1F2|=2c,
由椭圆、双曲线的定义得:|AF1|+|AF2|=2a1,|AF1|-|AF2|=2a2,
两式相加得:2|AF1|=2a1+2a2=4c,
即a1+a2=2c,两边同除以c得:$\frac{{a}_{1}}{c}+\frac{{a}_{2}}{c}=2$,
则$\frac{1}{\frac{c}{{a}_{1}}}+\frac{1}{\frac{c}{{a}_{2}}}=2$,所以$\frac{1}{{e}_{1}}+\frac{1}{{e}_{2}}=2$,
故选:D.
点评 本题考查椭圆与双曲线的标准方程及其性质、离心率计算公式,考查化简、变形能力,属于中档题.

练习册系列答案
相关题目
2.设f(x)=$\left\{\begin{array}{l}{\frac{2}{3}{x}^{3},x≤1}\\{{x}^{2},x>1}\end{array}\right.$,则f(x)在x=1处的( )
| A. | 左、右导数都存在 | B. | 左导数存在,右导数不存在 | ||
| C. | 左导数不存在,右导数存在 | D. | 左、右导数都不存在 |
19.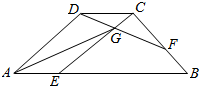 如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
 如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )
如图,在梯形ABCD中,AB=3CD=4AE,BC=3BF,DF交EC于点G,若$\overrightarrow{AG}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$,则$\frac{m}{n}$等于( )| A. | $\frac{11}{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{14}{33}$ | D. | $\frac{35}{56}$ |
6.已知直线y=kx-k及抛物线y2=2px(p≥0),则( )
| A. | 直线与抛物线有一个公共点 | B. | 直线与抛物线有两个公共点 | ||
| C. | 直线与抛物线有一个或两个公共点 | D. | 直线与抛物线可能没有公共点 |