题目内容
6．已知直线y=kx-k及抛物线y2=2px（p≥0），则（ ）| A． | 直线与抛物线有一个公共点 | B． | 直线与抛物线有两个公共点 | ||
| C． | 直线与抛物线有一个或两个公共点 | D． | 直线与抛物线可能没有公共点 |
分析 求出直线系经过的定点，判断点与抛物线的位置关系，即可推出结果．
解答 解：直线y=kx-k恒过（1，0）点，（1，0）在抛物线线y2=2px（p≥0）的内部，当k=0时，直线与抛物线只有一个交点，k不为0时，直线与抛物线有2个交点．
故选：C．
点评 本题考查张筱雨抛物线的位置关系的判断，基本知识的考查．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
16．一个几何体的三视图如图所示，则这个几何体的体积等于（ ）
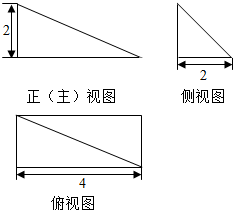
| A． | 12 | B． | 4 | C． | $\frac{16}{3}$ | D． | $\frac{8\sqrt{3}}{3}$ |
14．函数y=2sin（2x+$\frac{π}{3}$）的图象向左平移m（m＞0）个单位长度后，所得到的图象关于y轴对称，则m的最小值是（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{6}$ |
11．已知椭圆C1与双曲线C2具有相同的焦点F1，F2，A为C1与C2的一个公共点，△AF1F2为等腰三角形，设椭圆C1与双曲线C2的离心率分别为e1，e2，则（ ）
| A． | e1e2=1 | B． | e1e2=2 | C． | e1+e2=2 | D． | $\frac{1}{{e}_{1}}$+$\frac{1}{{e}_{2}}$=2 |
18．已知椭圆的焦点为F1（0，-1）和F2（0，1），点P（$\frac{2\sqrt{5}}{5}$，2）在椭圆上，则椭圆的短轴长为（ ）
| A． | 2 | B． | 2$\sqrt{3}$ | C． | 4 | D． | 6 |