题目内容
已知椭圆E:
+
=1(a>b>0)过点Q(1,-
),且离心率e=
,直线l与∑相交于M、N两点,l与x轴、y轴分别相交于C、D两点,O为坐标原点.
(1)求椭圆E的方程;
(2)判断是否存在直线l,满足2
=
+
2
=
+
,若存在,求出直线l的方程,若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
(1)求椭圆E的方程;
(2)判断是否存在直线l,满足2
| OC |
| OM |
| OD |
| OD |
| ON |
| OC |
考点:直线与圆锥曲线的综合问题
专题:向量与圆锥曲线
分析:(1)把点的坐标代入椭圆方程,结合椭圆的离心率及隐含条件列方程组求得a,b的值,则椭圆方程可求;
(2)把给出的向量等式变形,得到C、D为M、N的三等分点,设出直线l的方程y=kx+m(k≠0),和椭圆方程联立,利用四个点坐标间的关系求得k,代入关于x的方程后求得M的坐标,再由中点坐标公式列式求得m的值,则直线方程可求.
(2)把给出的向量等式变形,得到C、D为M、N的三等分点,设出直线l的方程y=kx+m(k≠0),和椭圆方程联立,利用四个点坐标间的关系求得k,代入关于x的方程后求得M的坐标,再由中点坐标公式列式求得m的值,则直线方程可求.
解答:
解:(1)由已知得:
,解得:a2=2,b2=1.
∴椭圆E的方程为
+y2=1;
(2)如图,
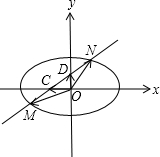 假设存在直线l:y=kx+m(k≠0)交椭圆于M(x1,y1),N(x2,y2)两点,交x轴于C(c,0),交y轴于D(0,d),
假设存在直线l:y=kx+m(k≠0)交椭圆于M(x1,y1),N(x2,y2)两点,交x轴于C(c,0),交y轴于D(0,d),
由2
=
+
,2
=
+
,得
=
,
=
,
即C、D为线段MN的三等分点.
由y=kx+m,取y=0,得c=-
,即C(-
,0),
取x=0,得d=m,即D(0,m).
联立
,得(1+2k2)x2+4kmx+2m2-2=0 ①.
∴x1+x2=-
,
若C、D为线段MN的三等分点,则-
=-
,解得:k2=
,k=±
.
当k=
时,方程①化为2x2+2
mx+2m2-2=0.
解得:x1=
,x2=
.
由
=-2
,解得:m=±
.
同理求得当k=
时,m=±
.
∴满足条件的直线l存在,方程为:y=±
+
或y=±
x-
.
|
∴椭圆E的方程为
| x2 |
| 2 |
(2)如图,
 假设存在直线l:y=kx+m(k≠0)交椭圆于M(x1,y1),N(x2,y2)两点,交x轴于C(c,0),交y轴于D(0,d),
假设存在直线l:y=kx+m(k≠0)交椭圆于M(x1,y1),N(x2,y2)两点,交x轴于C(c,0),交y轴于D(0,d),由2
| OC |
| OM |
| OD |
| OD |
| ON |
| OC |
| MC |
| CD |
| ND |
| DC |
即C、D为线段MN的三等分点.
由y=kx+m,取y=0,得c=-
| m |
| k |
| m |
| k |
取x=0,得d=m,即D(0,m).
联立
|
∴x1+x2=-
| 4km |
| 1+2k2 |
若C、D为线段MN的三等分点,则-
| 4km |
| 1+2k2 |
| m |
| k |
| 1 |
| 2 |
| ||
| 2 |
当k=
| ||
| 2 |
| 2 |
解得:x1=
-
| ||||
| 2 |
-
| ||||
| 2 |
由
-
| ||||
| 2 |
| m | ||||
|
| ||
| 5 |
同理求得当k=
| ||
| 2 |
| ||
| 5 |
∴满足条件的直线l存在,方程为:y=±
| ||
| 2 |
| ||
| 5 |
| ||
| 2 |
| ||
| 5 |
点评:本题考查了椭圆方程的求法,考查了直线与圆锥曲线的关系,训练了利用平面向量求解与圆锥曲线有关的问题,考查了数学转化思想方法,是压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设i是虚数单位,集合M={1,i},N={
,-
},则M∪N=( )
| (1-i)2 |
| 2 |
| 1 |
| i |
| A、M | B、N |
| C、{1,i,-i} | D、{1,i,-1} |
