题目内容
18.已知直线l1:2x-3y+1=0,直线l2过点(1,1)且与直线l1垂直.(1)求直线l2的方程;
(2)求直线l2与两坐标轴围成的三角形的面积.
分析 (1)求出l1的斜率,根据直线的垂直关系求出l2的斜率,从而求出l2的方程即可;(2)分别求出l2和坐标轴的交点,求出三角形的面积即可.
解答 解:(1)直线l1的斜率是$\frac{2}{3}$,
由l1⊥l2,得l2的斜率是-$\frac{3}{2}$,
故l2的方程是:y-1=-$\frac{3}{2}$(x-1),
即:3x+2y-5=0;
(2)由(1)l2的方程是:3x+2y-5=0,
令x=0,解得:y=$\frac{5}{2}$,
令y=0,解得:x=$\frac{5}{3}$,
故S△=$\frac{1}{2}$×$\frac{5}{2}$×$\frac{5}{3}$=$\frac{25}{12}$.
点评 本题考查了求直线方程问题,考查三角形的面积,是一道基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
8.在等差数列{an}中,a3+a8=-3,那么S10等于( )
| A. | -9 | B. | -11 | C. | -13 | D. | -15 |
6.设f(x)是定义在正整数集上的函数,且f(x)满足:“当f(k)>k2成立时,总可推出f(k+1)>(k+1)2成立”.那么,下列命题总成立的是( )
| A. | 若f(1)≤1成立,则f(9)≤81成立 | |
| B. | 若f(2)≤4成立,则f(1)>1成立 | |
| C. | 若f(3)>9成立,则当k≥1时,均有f(k)>k2成立 | |
| D. | 若f(3)>16成立,则当k≥3时,均有f(k)>k2成立 |
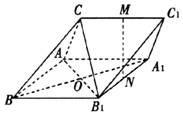 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.