题目内容
关于x的不等式ax2+bx+2>0的解集为(-
,
),则不等式
>6的解集为 .
| 1 |
| 2 |
| 1 |
| 3 |
| a(x-1) |
| x+b |
考点:其他不等式的解法,一元二次不等式的解法
专题:不等式的解法及应用
分析:由题意可得
,解得a、b的值,则不等式
>6,可化为
<0,(3x-4)(x-2)<0,由此求得它的解集.
|
| a(x-1) |
| x+b |
| 3x-4 |
| x-2 |
解答:
解:由题意可得
,
解得
.
∴不等式
>6,
即
>6,
即
>1.
化简可得
<0,
即 (3x-4)(x-2)<0.
解得
<x<2,
故答案为:(
,2).
|
解得
|
∴不等式
| a(x-1) |
| x+b |
即
| -12(x-1) |
| x-2 |
即
| -2(x-1) |
| x-2 |
化简可得
| 3x-4 |
| x-2 |
即 (3x-4)(x-2)<0.
解得
| 4 |
| 3 |
故答案为:(
| 4 |
| 3 |
点评:本题主要考查一元二次不等式的解法、分式不等式的解法,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
设a=0.6
,b=0.7
,c=lg
,则a,b,c之间的关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、c<a<b |
| B、b<a<c |
| C、c<b<a |
| D、a<b<c |
下列各式的值大于
的是( )
| 3 |
| 2 |
A、cos
| ||||||
| B、sin810°+tan765°-cos360° | ||||||
| C、sin(-1740°)cos1470°+cos(-660°)sin750°+tan405° | ||||||
D、sin 2
|
在区间[-1,1]上任取两个实数x,y,则满足x2+y2≥1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
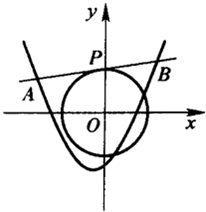 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;