题目内容
已知椭圆C:
+
=1的左、右焦点分别为F1、F2,P是椭圆上动点.
(1)求|PF1|•|PF2|的最大值;
(2)∠F1PF2=60°时,求△F1PF2的面积S;
(3)已知点A(2,2),求|PA|+|PF2|的最小值.
| x2 |
| 25 |
| y2 |
| 9 |
(1)求|PF1|•|PF2|的最大值;
(2)∠F1PF2=60°时,求△F1PF2的面积S;
(3)已知点A(2,2),求|PA|+|PF2|的最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设P(x,y),由焦半径公式|PF1|•|PF2|=(a+ex)(a-ex),能求出|PF1|•|PF2|的最大值.
(2)由椭圆的焦点三角形面积公式△F1PF2的面积S=b2tan
,能求出△F1PF2的面积.
(3)由已知条件推导出当且仅当P、A、F1共线时|PA|+|PF2|取最小值,由此能求出这个最小值.
(2)由椭圆的焦点三角形面积公式△F1PF2的面积S=b2tan
| θ |
| 2 |
(3)由已知条件推导出当且仅当P、A、F1共线时|PA|+|PF2|取最小值,由此能求出这个最小值.
解答:
解:(1)∵椭圆C:
+
=1的左、右焦点分别为F1、F2,P是椭圆上动点,
∴a=5,b=3,c=4,e=
=
,F1(-4,0),F2(4,0)
设P(x,y),由焦半径公式,
|PF1|•|PF2|=(a+ex)(a-ex)=25-
,
∴当x=0时,|PF1|•|PF2|的最大值为25.
(2)∵∠F1PF2=60°,
由椭圆的焦点三角形面积公式:
△F1PF2的面积S=b2tan
=9•tan30°=3
,
∴△F1PF2的面积S=3
.
(3)|PA|+|PF2|=|PA|+(2a-|PF1|)=2a+(|PA|-|PF1|),
由于-|AF1|≤|PA|-|PF1|≤|AF1|,
当且仅当P、A、F1共线时取等号,
∴|PA|+|PF2|的最小值=2a-|AF2|=10-
=10-2
.
| x2 |
| 25 |
| y2 |
| 9 |
∴a=5,b=3,c=4,e=
| c |
| a |
| 4 |
| 5 |
设P(x,y),由焦半径公式,
|PF1|•|PF2|=(a+ex)(a-ex)=25-
| 16x2 |
| 25 |
∴当x=0时,|PF1|•|PF2|的最大值为25.
(2)∵∠F1PF2=60°,
由椭圆的焦点三角形面积公式:
△F1PF2的面积S=b2tan
| θ |
| 2 |
| 3 |
∴△F1PF2的面积S=3
| 3 |
(3)|PA|+|PF2|=|PA|+(2a-|PF1|)=2a+(|PA|-|PF1|),
由于-|AF1|≤|PA|-|PF1|≤|AF1|,
当且仅当P、A、F1共线时取等号,
∴|PA|+|PF2|的最小值=2a-|AF2|=10-
| (-4-2)2+(0-2)2 |
| 10 |
点评:本题考查椭圆中两条线段长的乘积的最大值的求法,考查三角形面积的求法,考查两条线段和的最小值的求法,解题时要熟练掌握椭圆的简单性质.

练习册系列答案
相关题目
在平面直角坐标系中,定点M(1,0),两动点A,B在双曲线x2-3y2=3的右支上,则cos∠AMB的最小值是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
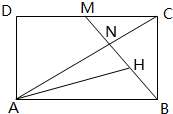 如图,M是矩形ABCD的边CD上的一点,AC与BM相交于点N,BN=
如图,M是矩形ABCD的边CD上的一点,AC与BM相交于点N,BN=