题目内容

从圆（x-1）2+y2=1外一点P（2，4）引这个圆的切线，则此切线方程为
 
．
考点：圆的切线方程
专题：直线与圆
分析：由题意画出图形，分切线的斜率存在和不存在求切线方程，当斜率存在时由圆心到切线的距离等于半径求得切线的斜率，则答案可求．
解答： 解：如图，

当切线的斜率不存在时，切线方程为x=2；
当切线的斜率存在时，设斜率为k，则切线方程为y-4=k（x-2），即kx-y-2k+4=0．
由圆心M（1，0）到切线的距离等于半径得：
|k-2k+4|
k2+1
=1，解得k=
15
8
．
∴斜率存在时的切线方程为15x-8y+2=0．
故答案为：x=2或15x-8y+2=0．
点评：本题考查了圆的切线方程，考查了直线和圆的位置关系，解答直线与圆的切线问题，一般用圆心到直线的距离等于半径解决，是基础题．
练习册系列答案
相关题目
已知函数f（x）=ln（
1
2
+
1
2
ax）+x2-ax（a为常数，a＞0）．
（1）若x=-
1
2
是函数f（x）的一个极值点，求a的值；
（2）求证：当0＜a≤2时，f（x）在[
1
2
，+∞）上是增函数．
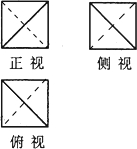正方体的四个顶点构成的几何体的三视图如图，若各视图均为边长为2的正方形，则这个几何体的体积是（　　）
A、
4
3
B、
8
3
C、
16
3
D、
20
3
函数y=lg（2sinx-
3
）的定义域为
 
．
y=2x2-1在[1，3]上的最小值是
 
，最大值为
 
，值域为
 
．
若函数y=2sin（x+m-
π
6
）的图象关于y轴对称，则实数m（m＞0）的最小值为
 
．
如图，已知AB是半圆O的直径，AB=8，M，N，P是将半圆圆周四等分的三个分点，从A，B，M，N，P这5个点中任取3个点，则这3个点组成直角三角形的概率为（　　）
A、
7
10
B、
1
2
C、
3
10
D、
1
10
过定点（1，2）一定可作两条直线与圆x2+y2+kx+2y+k2-15=0相切，则k的取值范围是
 
．
在△ABC中，a，b，c分别是角A，B，C的对边，且满足acosA=bcosB，那么△ABC的形状一定是 （　　）
A、等腰三角形
B、直角三角形
C、等腰或直角三角形
D、等腰直角三角形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网