题目内容
y=2x2-1在[1,3]上的最小值是 ,最大值为 ,值域为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:根据二次函数的性质先求出函数的单调性,从而求出函数的最大值,最小值,进而求出函数的值域.
解答:
解:∵y=2x2-1在[1,3]上单调递增,
∴x=1时,y最小为1,x=3时,y最大为17,
故答案为:1,17,[1,17].
∴x=1时,y最小为1,x=3时,y最大为17,
故答案为:1,17,[1,17].
点评:本题考查了二次函数的性质,考查了函数的最值问题,是一道基础题.

练习册系列答案
相关题目
已知函数f(x)=
+x(a∈R)在[2,+∞)上单调递增,则a的取值范围是( )
| a |
| x |
| A、(0,4) |
| B、(-∞,4] |
| C、(0,2) |
| D、(-∞,2] |
若用m,n表示两条不同的直线,用α表示一个平面,则下列命题正确的是( )
| A、若m∥n,n?α,则m∥α |
| B、若m∥α,n?α,则m∥n |
| C、若m⊥n,n?α,则m⊥α |
| D、若m⊥α,n?α,则m⊥n |
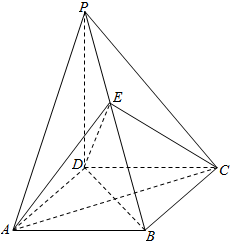 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=