题目内容
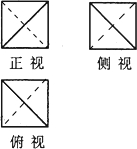 正方体的四个顶点构成的几何体的三视图如图,若各视图均为边长为2的正方形,则这个几何体的体积是( )
正方体的四个顶点构成的几何体的三视图如图,若各视图均为边长为2的正方形,则这个几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据几何体的三视图,得出该几何体是棱长为2的正方体切去了四个全等的小三棱锥,求出体积即可.
解答:
解:把三视图还原成原图如图所示;
是一个棱长为2的正方体切去了四个全等的小三棱锥;
所以体积V=23-4×
×
×2×2×2=
.
故选:B.

是一个棱长为2的正方体切去了四个全等的小三棱锥;
所以体积V=23-4×
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
故选:B.
点评:本题考查了空间几何体的三视图的应用问题,是基础题目.

练习册系列答案
相关题目
已知圆的方程式x2+y2=36,记过点P(1,2)的最长弦和最短弦分别为AB、CD,则直线AB、CD的斜率之和等于( )
| A、-1 | ||
B、
| ||
| C、1 | ||
D、-
|
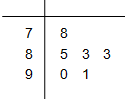 为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是( )
为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是( )| A、中位数为83 |
| B、平均数为85 |
| C、众数为85 |
| D、方差为19 |
若对任意一点O和不共线的三点A、B、C有
=x
+y
+z
,则x+y+z=1是四点P、A、B、C共面的( )
| OP |
| OA |
| OB |
| OC |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
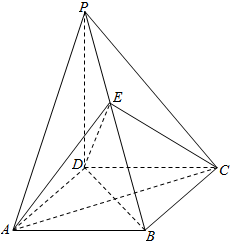 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=